-Werkstatt - Volltexte im HTML-Format - kostenlos
-->Übersicht -->Alphabetische Liste aller Texte -->Info zu dieser Website -->Lexikon -->Startseite
Das Mehrheitsprinzip
Zur Methodologie der normativen
Sozialwissenschaften:
Tauschprinzip - Mehrheitsprinzip - Gesamtinteresse
Teil III, 1976
*** Empfehlung: Nutzen Sie die Suchfunktion Ihres Internet-Browsers! ***
Vorbemerkung:
Der folgende Text enthält Teil III , Kap. 17-24, der Arbeit:
"Zur Methodologie
der normativen Sozialwissenschaften.
Tauschprinzip - Mehrheitsprinzip -
Gesamtinteresse"
aus dem Jahr 1976.
Im
Klett-Cotta-Verlag erschien 1979 eine überarbeitete und gekürzte Fassung dieser Arbeit unter
dem geänderten Titel:
"Tauschprinzip - Mehrheitsprinzip - Gesamtinteresse. Zur Methodologie
normativer Ökonomie und Politik".
Dieses Buch ist als PDF-Datei hier verfügbar.
Der vorliegende Text schließt an
folgende Abschnitte an:
Teil I (Kap. 1-11): Einzelinteresse und
Gesamtinteresse *** (598 K)
und
Teil II Kap. 12: Einstimmigkeits-Regeln und
Status-quo-Klauseln ** (68 K).
Teil II Kap. 13-16: Das Modell der Marktwirtschaft. Darstellung und Kritik *** (239 K)
Die ursprünglichen Seitenzahlen sind in geschweiften Klammern eingefügt. Die
Fußnoten wurden in den Text eingearbeitet und sind an der Kursivschrift zu
erkennen.
Diejenigen Paragraphen, die im Inhaltsverzeichnis mit einem grünen
Sternchen (*) gekennzeichnet sind, wurden in der
Buchausgabe von 1979 weggelassen.
Inhaltsverzeichnis:
Teil III: DAS MEHRHEITSPRINZIP
17. Kapitel
Die Abstimmung als Ausdruck des individuellen Interesses oder als Urteil über das Gesamtinteresse?
§ 106 Die aggregative und die selektive Verwendung des
Mehrheitsprinzips 497
§ 107 Die wahrscheinlichkeitstheoretische Rechtfertigung
des selektiven Mehrheitsprinzips 498
§ 108 ROUSSEAUS Auffassung des Mehrheitsprinzips 500
18. Kapitel
Die Mehrheitsalternative
§ 110 Das Mehrheitsprinzip und die Bestimmung der
Mehrheitsalternative 514
19. Kapitel
Abstimmungsverfahren und die Auswirkungen von Koalitionsbildung
§ 112 Entscheidungsregel und konkretes
Entscheidungsverfahren 528
§ 113 Die Regel der relativen Mehrheit bei einmaliger
Abstimmung 529
§ 114 Eigeninteressierte Koalitionsbildung im relativen
Mehrheitssystem 533
§ 115 Die Regel der absoluten Mehrheit
538*
§ 116 Das Verfahren der 'schrittweisen Eliminierung' der
Alternativen 542*
§ 117 Die Rangplatz-Methode der Abstimmung 547*
§ 118 Die Punkte-Methode der Abstimmung 554*
§ 119 Das Verfahren der 'paarweisen Abstimmung’ 557*
20. Kapitel
Abstimmungsstrategien isolierter Individuen
§ 121 Die spieltheoretische Analyse individueller
Abstimmungsstrategien bei FARQUHARSON 565*
§ 122 "Ausgeklügelte" individuelle Abstimmungsstrategien 570*
§ 123 Möglichkeiten eines strategischen Dilemmas 575*
21. Kapitel
Abstimmungsstrategien bei Serien von Entscheidungen im Mehrheitssystem
§ 125 Der Stimmentausch 582
§ 126 Stimmentausch oder Koalitionsbildung? 590
§ 127 Probleme eines "marktmäßigen" Stimmentauschs und die
Vorteile von Abstimmungskoalitionen 592*
§ 128 Einzel-Punkt-Koalitionen und Mehr-Punkte-Koalitionen 599*
§ 129 Rationale Koalitionsbildung bei Entscheidungsserien
und die Durchsetzung des Mehrheitsalternativenbündels 602
22. Kapitel
Die normative Beurteilung des Mehrheitssystems
§ 131 Mehrheitsprinzip und Gleichgewichtung der
individuellen Präferenzen 612
§ 132 Weitere Eigenschaften des Mehrheitsprinzips 615
§ 133 Mehrheitsprinzip und kollektive Betroffenheit von
Entscheidungen 618
§ 134 Der Informations- und Entscheidungsaufwand im
Mehrheitssystem 619
§ 135 Mehrheitsprinzip und Status-quo-Klausel 621*
§ 136 Zyklische Mehrheiten und das Problem der Instabilität im
Mehrheitssystem 622
§ 137 Nutzenmäßige Interdependenzen zwischen verschiedenen
Entscheidungen 631
§ 138 Die Nicht-Berücksichtigung von Präferenzintensitäten 634
1. Intensitätsberücksichtigung bei Einzelentscheidungen 634
2. Intensitätsberücksichtigung bei Entscheidungsserien 637
23. Kapitel
Berücksichtigung von Präferenzintensitäten im Mehrheitssystem
§ 140 Die Anhebung der erforderlichen Mehrheit 646
§ 141 Die Einführung individueller Abstimmungskosten 651*
24. Kapitel
§ 143 Zusammenfassung und Schluss 657
Literatur-Verzeichnis 664-686
Textbeginn
zum Anfang
Teil III
Das Mehrheitsprinzip
{495}
Wie im Teil II Kapitel 12 (Einstimmigkeits-Regeln
und Status-quo-Klauseln) ausgeführt wurde, führt die Einstimmigkeits-Regel auch in der Form des Pareto-Kriteriums gewöhnlich zu keiner Entscheidung hinsichtlich der zu
wählenden Alternative, da meist keine Alternative von allen Individuen als die
beste entsprechend ihrem individuellen Interesse angesehen wird.
Eine Möglichkeit zur Behebung dieses Problems ist die Modifizierung der reinen
Einstimmigkeits-Regel durch eine Status-quo-Klausel sowie durch die Abgrenzung
separater Verfügungsbereiche. Sofern die individuellen Interessen durch die
betreffenden Individuen autonom bestimmt werden, ergibt sich daraus das Eigentum-Vertrags-System, das im Teil II diskutiert wurde.
Ein anderer Weg zur Bildung eines
kollektiven Gesamtwillens ist die Mehrheitsregel. Dabei wird die Forderung nach
einer einstimmigen Befürwortung der zu wählenden Handlungsalternative insofern
gelockert, als nur noch ihre Befürwortung durch eine Mehrheit der Individuen und
nicht mehr durch alle verlangt wird.
Gewöhnlich wird auch das Mehrheitsprinzip
in der Form eines individualistischen Entscheidungs-Systems praktiziert, in dem
die betreffenden Individuen ihre Interessen autonom bestimmen. Dann stellt sich
auch hier die Frage nach der Qualifikation der individuellen
Interessenäußerungen. Da diese Frage jedoch bereits gesondert abgehandelt wurde,
wird im Folgenden von dieser Problematik weitgehend abgesehen.[[1]
Siehe oben § 69.]
{496} Bevor nun die verschiedenen Varianten des Mehrheitsprinzips näher analysiert werden, muss vorweg noch auf die grundsätzliche Frage nach der Interpretation des Mehrheitsprinzips eingegangen werden. In der Theoriegeschichte werden hierfür nämlich zwei unterschiedliche Deutungen gegeben. Das eine Mal wird das Abstimmungsverhalten eines Individuums nur als Ausdruck seines individuellen Interesses gesehen, während es das andere Mal als Urteil des Individuums über das Gesamtinteresse interpretiert wird. Beide Varianten sollen im folgenden Abschnitt näher untersucht werden.{497}
17. Kapitel
Die Abstimmung als Ausdruck des individuellen Interesses oder als Urteil über das Gesamtinteresse
§ 106 Die aggregative und die selektive Verwendung des Mehrheitsprinzips
Bei der einen Interpretation des Mehrheitsprinzips wird davon ausgegangen,
dass
die Individuen bei den Abstimmungen ihr individuelles Interesse ausdrücken,
wobei die Alternative mit den zahlreichsten Befürwortern unter bestimmten
Voraussetzungen als eine Annäherung an ein solidarisch bestimmtes
Gesamtinteresse aufgefasst werden kann.
Man kann Abstimmungen nach dem Mehrheitsprinzip jedoch
auch so interpretieren, dass dabei jedes Individuum unmittelbar seine Auffassung
vom Gesamtinteresse ausdrückt. Bei unterschiedlichen Auffassungen vom
Gesamtinteresse wird die Auffassung der Mehrheit als das wahrscheinlich richtige
Urteil angesehen.
Während im ersteren Falle jedes Individuum eigentlich mit
seiner Stimmabgabe auf eine andere Frage antwortet, nämlich welche Alternative
seinen jeweils eigenen Interessen am besten entspricht, antworten im letzteren
Fall alle Individuen auf die gleiche Frage danach, welche Alternative dem
Gesamtinteresse am besten entspricht. Während das Mehrheitsprinzip im ersten
Fall eine Aggregationsfunktion hat - es aggregiert die geäußerten individuellen
Interessen zum Gesamtinteresse - , hat es im zweiten Fall eine
Selektionsfunktion - es wählt unter verschiedenen Auffassungen vom Gesamtinteresse die
wahrscheinlich richtige aus. {498}
Ein Beispiel für die selektive Verwendung des
Mehrheitsprinzips ist die mehrheitlich gefällte Entscheidung eines
Richterkollegiums bzw. einer Jury, die zu beurteilen hat, ob ein Angeklagter die
ihm zur Last gelegte Tat begangen hat oder nicht. Wenn sich die beteiligten
Richter oder Geschworenen nicht darüber einig sind, kann man zur verbindlichen
Auffassung der gesamten Jury diejenige Auffassung erklären, die von der Mehrheit
ihrer Mitglieder geteilt wird. [[2] So wird z. B. im Bundesverfassungsgericht der
Bundesrepublik verfahren, wo auch die Abstimmungsverhältnisse mitgeteilt werden.
S. MODEL/CREIFELDS 1973, S.123.]
Es stellt sich jedoch die Frage, warum das Mehrheitsprinzip
geeignet sein soll, unter differierenden Urteilen verschiedener Individuen das
richtige herauszufinden. Die Auffassung, dass die Mehrheit immer recht hat, lässt
sich auf gar keinen Fall aufrechterhalten, wie zahlreiche Beispiele zeigen. Man kann jedoch die Auffassung vertreten,
dass zumindest unter
bestimmten Bedingungen die Wahrscheinlichkeit dafür, dass sich
die Mehrheit irrt, geringer ist als die Wahrscheinlichkeit dafür, dass sich die
Minderheit oder jeder Einzelne irrt.
§ 107 Die wahrscheinlichkeitstheoretische Rechtfertigung
des selektiven Mehrheitsprinzips
Die wahrscheinlichkeitstheoretische Argumentation zugunsten
eines selektiv verwendeten Mehrheitsprinzips wurde bereits 1785 von CONDORCET
in seinem 'Essai' {499} entwickelt. [[3]Siehe dazu die Darstellung bei BLACK
1971, S.159ff.] Ein Beispiel kann diese Überlegungen
verdeutlichen.
Angenommen ein Richterkollegium besteht aus 5 Richtern. Die
Wahrscheinlichkeit dafür, dass sich ein einzelner Richter hinsichtlich der Schuld
des Angeklagten irrt, betrage für jeden von ihnen 1:5 bzw. 20%. Dann beträgt die
Wahrscheinlichkeit dafür, dass sich alle 5 Richter gleichzeitig irren, gemäß der
Multiplikationsregel für unabhängige Ereignisse (0,2)5 = 0,00032 oder
0,032%. [[4] Siehe
CLAUSS/EBNER 1970, S.122f.]
Wie CONDORCET durch statistische Argumentation
nachgewiesen hat, steigt bei einer gegebenen Irrtumswahrscheinlichkeit der
Individuen und bei gegebener Größe der Jury die Wahrscheinlichkeit für ein
richtiges Urteil eines bestimmten Anteils der Jury mit der Größe dieses Anteils
an der Jury. [[5] Siehe die genaue Formel bei BLACK 1971, S.165.]
Folglich ist die Wahrscheinlichkeit für ein richtiges Urteil einer Mehrheit
größer als die Wahrscheinlichkeit für ein richtiges Urteil einer Minderheit. "Solange angenommen wird, dass jeder eine gleiche Chance von mehr
als 50% dafür hat, die richtige Antwort zu geben, wird das Mehrheitsurteil (auf
die Dauer) häufiger richtig sein als das Urteil irgendeines bestimmten Wählers.
... Wenn wir eine Wählerschaft von 1 000 haben, von der jedes Mitglied im
Durchschnitt in 51% der Fälle richtig urteilt, wie groß ist dann die
Wahrscheinlichkeit dafür, dass in einem bestimmten Fall eine Mehrheit von 51% die
richtige Antwort gibt? {500} Die Antwort lautet - vielleicht etwas überraschend: mehr
als 2 zu 1 (69%). Mehr noch, wenn die erforderliche Mehrheit bei 51% bleibt und
die Zahl der Wähler auf 10 000 erhöht wird, oder wenn die Zahl der Wähler bei 1
000 bleibt und die erforderliche Mehrheit auf 60% erhöht wird, steigt die
Wahrscheinlichkeit dafür, dass die Mehrheit .. die richtige Antwort hat,
praktisch auf 1 (99,97%)." [[6] BARRY 1964, S.122.]
Es stellt sich die Frage, ob man auch die normsetzenden Abstimmungen im Zuge eines sozialen Willensbildungsprozesses als
Selektion der richtigen Auffassung vom Gesamtinteresse interpretieren kann. Wie
BLACK ausführt, war CONDORCET selber dieser Meinung. "Eine Theorie, die das
Jury-Problem hinreichend erfasst, würde nach CONDORCETs Meinung auch geeignet
sein, um Gremien jeglicher Art zu behandeln, z. B. parlamentarische
Körperschaften und lokale Organe. ... Von jedem Wähler wird angenommen, dass eine
bestimmte Wahrscheinlichkeit dafür besteht, dass er ein richtiges Urteil in Bezug
auf die Kandidaten abgibt, zwischen denen er auswählt." [[7]
BLACK 1971, S.163.]
§ 108 ROUSSEAUS Auffassung des Mehrheitsprinzips
Eine derartige selektive Interpretation des
Mehrheitsprinzips war bereits 1762 von ROUSSEAU (1712-78) in seinem "Gesellschaftsvertrag"
vertreten worden. "Bei einem Gesetzesvorschlag in der Volksversammlung fragt man
sie (die Staatsbürger, E.W.) nicht eigentlich, ob {501} sie dem Vorschlag zustimmen oder ihn verwerfen, sondern ob
er dem allgemeinen Willen entspricht oder nicht. ... Wenn mithin meine Ansicht
der entgegen gesetzten unterliegt, so beweist dies nichts anderes, als dass ich
mich geirrt hatte, und dasjenige, was ich für den allgemeinen Willen hielt, es
nicht war." [[8] ROUSSEAU 1968, S.154.]
Dass bei einer Abstimmung nach dem Mehrheitsprinzip die
Individuen nicht die Frage nach ihrem jeweiligen individuellen Interesse sondern
die Frage nach dem Gesamtinteresse beantworten sollen, macht ROUSSEAU auch am
Beispiel eines Staatsbürgers klar, der seine Stimme für Geld verkauft. "Der
Fehler, den er begeht, besteht in der Änderung der Fragestellung; er antwortet
auf etwas ganz anderes, als er gefragt ist. Anstatt durch die Abgabe seiner
Stimme zu sagen: 'Es ist dem Staat vorteilhaft', sagt er: 'Es ist diesem oder
jenem Manne, dieser oder jener Partei vorteilhaft, dass dieser oder jener Antrag
durchgeht'." [[9] ROUSSEAU 1968, S.151.]
Die Individuen sollen bei der Abstimmung also nicht ihr
individuelles Interesse, sondern ihre Auffassung vom Gesamtinteresse ausdrücken,
wobei gewöhnlich davon auszugehen ist, dass sich die Minderheit irrt.
Im Gegensatz zu CONDORCET findet sich bei ROUSSEAU jedoch
kein ausdrücklicher Beweis dafür, dass die Mehrheit eher in der Lage ist als die
Minderheit, den allgemeinen Willen bzw. das Gesamtinteresse zu erkennen.
Unausgesprochen scheinen jedoch ähnliche Annahmen zugrunde zu liegen.
Im
Idealfall eines intakten Gemeinwesens ist für ROUSSEAU die Einstimmigkeit {502} bei der Beschlussfassung über Gesetze anzustreben bzw.
diese stellt sich von selber her. "Solange mehrere Menschen sich als einen
einzigen Körper betrachten, haben sie nur einen einzigen Willen, der die
gemeinsame Erhaltung und die allgemeine Wohlfahrt zum Gegenstand hat. ... Das
Gemeinwohl tritt überall sichtbar hervor, und es bedarf nur gesunder Vernunft,
um es wahrzunehmen. ... Sobald die Privatinteressen sich immer mehr geltend zu
machen und die kleinen Gesellschaften auf die große einzuwirken anfangen: dann
leidet das gemeinsame Interesse und findet Gegner; es herrscht keine
Einstimmigkeit mehr; der allgemeine Wille ist nicht mehr der Wille aller; es
erheben sich Widersprüche und Streitigkeiten und die beste Ansicht wird nicht
ohne lebhafte Wortgefechte angenommen." [[10] ROUSSEAU 1968, S.149f.]
Für ROUSSEAU ist die Verwendung des Mehrheitsprinzips also
nur ein Notbehelf, wo unter dem Einfluss der Privatinteressen oder
Gruppeninteressen das Gesamtinteresse nicht mehr von allen verfolgt wird. Nehmen
diese Privatinteressen überhand, so bedeutet das den Niedergang des
Gemeinwesens, und auch die Stimmenmehrheit hat dann nicht mehr "die Kennzeichen
des allgemeinen Willens an sich. ... Sind diese im Schwinden begriffen, so gibt
es keine Freiheit mehr, welche Partei man auch ergreife." [[11]
ROUSSEAU 1968, S.154f.]
Weiterhin erscheint
ROUSSEAU ein Abgehen vom Prinzip der Einstimmigkeit bei weniger wichtigen sowie
bei eiligen Beschlüssen geboten: "Je wichtiger und ernster die Beschlüsse
sind, um so mehr muss der gültige Beschluss sich der Einstimmigkeit nähern; ... je
größere Beschleunigung {503} die zur Beratung gelangte Angelegenheit erfordert, um so mehr
muss man das bei Meinungsverschiedenheit vorgeschriebene Mehrheitsverhältnis
einschränken. [[12] ROUSSEAU 1968, S.135.] Wenn die Individuen bei einer Entscheidung unterschiedlich
abstimmen, so dürfen sich nach ROUSSEAU darin höchstens
Meinungsverschiedenheiten über das Gesamtinteresse, jedoch keine individuellen
Interessengegensätze ausdrücken.
Verschiedene Autoren haben ROUSSEAU daraufhin
den Vorwurf einer totalitären Doktrin gemacht, bei dem die partikularen
Interessen zugunsten eines vorweg gesetzten Gemeinwohls unterdrückt werden. [[13]
So z. B. TALMON 1970, S.38ff. u.
FRAENKEL 1964, S.205ff.]
Demgegenüber ist BARRY der Ansicht, dass ROUSSEAU immer die
Voraussetzung einer
Interessengleichheit aufgrund sozialer Homogenität in den öffentlichen
Angelegenheiten gemacht hat. "Unter den verschiedenen Alternativen, die
jedermann in der gleichen Weise betreffen, muss jede Person entscheiden, welche
ihm selbst am meisten Vorteile bringt - und da jedermann sonst in ähnlichen
Umständen ist, entscheidet er damit automatisch für das, was jedem andern die
meisten Vorteile bringen würde." [[14] BARRY 1964, S.121f.]
In neuerer Zeit hat auch RAWLS gefordert, dass die Individuen bei gesetzgebenden Abstimmungen nach dem Mehrheitsprinzip nicht ihre eigenen Interessen, sondern ihre Auffassungen vom Gemeinwohl bzw. einer gerechten Ordnung ausdrücken sollen. "Die gesetzgeberische Diskussion darf nicht als ein Streit zwischen Interessen aufgefasst werden, sondern als ein Versuch, {504} die beste Politik zu finden, so wie sie von den Prinzipien der Gerechtigkeit bestimmt wird." [[15] RAWLS 1973, S.357]
Wenn es bei Mehrheitsabstimmungen
nicht um den Ausdruck individueller Interessen geht, sondern um unterschiedliche
Beurteilungen der gerechtesten Alternative, so ist die unten ausführlich
diskutierte unterschiedliche Betroffenheit der Individuen von der Entscheidung
kein Problem mehr: "Es wird manchmal gegenüber der Mehrheitsregel eingewandt,
dass ... sie bei der Berücksichtigung der Stärke des Begehrens versagt, denn der
größere Teil kann sich über die starken Empfindungen einer Minderheit
hinwegsetzen. Diese Kritik beruht auf der irrigen Ansicht, dass die Intensität
des Begehrens ein wesentlicher Gesichtspunkt bei der Gesetzgebung sei. Im
Gegenteil, immer wenn Fragen der Gerechtigkeit gestellt werden, dürfen wir nicht
nach der Stärke der Empfindung verfahren, sondern müssen stattdessen die größere
Gerechtigkeit der gesetzlichen Ordnung anstreben. ... Die Stärke entgegen gesetzter Einstellungen hat keinen Einfluss auf die Frage, ob etwas recht
ist, sondern nur auf die Frage der Durchführbarkeit." [[16] RAWLS 1973, S.230f. Zu Präferenzintensitäten
s. u. § 138]
Wenn man die beiden Anwendungsformen des Mehrheitsprinzips
miteinander vergleicht - einmal zur Aggregation individueller Interessen und das
andere Mal zur Selektion der richtigen Auffassung vom Gesamtinteresse - , so
kann es nicht darum gehen, welche von beiden die allein "richtige" ist. Im
Prinzip sind beide Verfahren möglich.
Wenn man das Mehrheitsprinzip als Aggregationsmechanismus für die individuellen Interessen verwendet, so stellt
die gewählte {505} Mehrheitsalternative unter bestimmten Voraussetzungen ein
Maximum des Gesamtnutzens dar, denn das vom Eigeninteresse geleitete
Abstimmungsverhalten der Individuen führt dann quasi automatisch zur
Durchsetzung des Gesamtinteresses. [[17] Siehe hierzu unten § 139] Das
Gesamtinteresse ergibt sich hierbei also erst im Nachhinein als Resultat des Abstimmungsprozesses.
Im Prinzip kann man jedoch das Gesamtinteresse auch direkt
argumentativ bestimmen, wie oben anhand der Ausführungen zum Solidaritätsprinzip
und zur interpersonal vergleichbaren Messung der individuellen Nutzen dargelegt
wurde.[[18] Siehe dazu oben Kap.7] Insofern ist FRAENKEL nicht beizustimmen, wenn er mit Blick auf
ROUSSEAU meint, "in einer differenzierten Gesellschaft könne im Bereich der
Politik das Gemeinwohl lediglich a posteriori erreicht werden" und wenn er jede
direkte Bestimmung des Gemeinwohls dem Totalitarismus-Verdacht aussetzt. [[19]
FRAENKEL 1964, S.200] Um
überhaupt beurteilen zu können, ob ein politischer Prozess zu einer Realisierung
des Gemeinwohls führt, wie es auch FRAENKEL tut, muss man einen von diesem Prozess unabhängigen Begriff vom Gemeinwohl haben.
Wie in den Ausführungen zum
Solidaritätsprinzip gezeigt wurde, hat jedes Individuum im Prinzip die
Möglichkeit, sich selber eine Auffassung vom Gesamtinteresse zu bilden, über
deren Richtigkeit jedenfalls im Grundsatz ein argumentativer Konsensus
herstellbar ist. Insofern dieser Konsensus aber faktisch nicht immer erzielt
wird wegen der Möglichkeit von Irrtümern, eigeninteressierten {506} Verzerrungen oder Zeitdruck, hat das
Mehrheitsprinzip hier
nur noch die nachgeordnete Aufgabe, auch im Falle unterschiedlicher Auffassungen
vom Gesamtinteresse die wahrscheinlich richtige auszuwählen.
Sowohl die aggregative als auch die selektive Verwendung des Mehrheitsprinzips erscheint
also als prinzipiell möglich. Allerdings wirft die selektive Verwendung
besondere Probleme auf, die im Folgenden näher analysiert werden sollen.
§ 109 Problematische Konsequenzen einer selektiven Interpretation des Mehrheitsprinzips
Eine Schwierigkeit bei der selektiven Verwendung des
Mehrheitsprinzips liegt darin, dass dabei eine erheblich kompliziertere
Erkenntnisleistung der Individuen vorausgesetzt werden muss als bei der
aggregativen Verwendung. Bei der letzteren müssen die Individuen nur die Frage
beantworten können, welche der zur Entscheidung stehenden Alternativen in ihrem
eigenen Interesse ist. Selbst diese Leistung kann bereits problematisch sein,
sodass es besonderer institutioneller Vorkehrungen bedarf, um eine hinreichende
Aufklärung und Reflektion der Individuen über ihre eigene Interessenlage zu
gewährleisten. [[20] Siehe dazu oben Kap. 10]
Bei der selektiven Verwendung des Mehrheitsprinzips müssen die
Individuen mit ihrer Stimmabgabe jedoch auf die viel kompliziertere Frage
antworten können, welche der zur Entscheidung stehenden Alternativen dem
Gesamtinteresse am besten entspricht, d.h. sie müssen die Interessen aller
Beteiligten kennen und solidarisch gegeneinander {507} abwägen, um diese Frage richtig beantworten zu können.
Dies erscheint noch möglich, wenn das Kollektiv entweder
relativ wenig Individuen umfasst oder wenn es in sich sehr homogen ist, sodass jeder mit den
Lebensumständen und Bedürfnissen jedes andern vertraut ist, weil diese den
eigenen Verhältnissen ähnlich sind. Ein solches überschaubares Gemeinwesen mit
relativ gering differenzierter sozialer Struktur hatte offenbar ROUSSEAU vor
Augen, wenn er davon schreibt, dass "Scharen von Landsleuten die
Staatsangelegenheiten unter einer Eiche entscheiden. ... Ein auf solche Weise
regierter Staat hat nur wenige Gesetze nötig, und je notwendiger sich der Erlass
neuer macht, desto allgemeiner wird auch diese Notwendigkeit anerkannt. Wer sie
zuerst vorschlägt, spricht nur aus, was alle schon längst gefühlt (haben, E. W
.) . " [[21] ROUSSEAU 1968, S.149f. FRAENKEL wirft dieser Position
deshalb auch vor, "dass sie das Phänomen der differenzierten Gesellschaft
unbeachtet lasse - und wenn überhaupt - nur nach einer radikalen Revolution
verwendbar sei." FRAENKEL 1964, S.206]
In industrialisierten Großgesellschaften mit ihren
regionalen, kulturellen oder schichtenmäßigen Differenzierungen sowie ihren
komplizierten institutionellen Zusammenhängen kann man jedoch nicht mehr ohne
weiteres von ROUSSEAUs Annahme ausgehen, die er in die Worte fasst: "Das
Gemeinwohl tritt überall sichtlich hervor, und es bedarf nur gesunder Vernunft,
um es wahrzunehmen." [[22] ROUSSEAU 1968, S.149] Allerdings hat ROUSSEAU
recht, wenn er darauf hinweist, dass die Bestimmung des Gesamtinteresses {508} umso schwieriger wird, je schärfer die
Gesellschaft durch Standes- oder Klassenschranken bzw. durch soziale und
ökonomische Ungleichheit in gegensätzliche Privat- und Gruppeninteressen
gespalten ist.
Wenn es jedoch eine komplizierte Erkenntnisleistung
darstellt, das Gesamtinteresse einer differenzierten Gesellschaft zu erkennen,
so wird die Annahme problematisch, dass die Auffassung der Mehrheit hierzu
wahrscheinlich die richtige ist.
Die von CONDORCET entwickelte
wahrscheinlichkeitstheoretische Begründung für die selektive Verwendung des
Mehrheitsprinzips gilt nur unter bestimmten Voraussetzungen. Eine davon ist,
dass die Urteile der Individuen voneinander unabhängige Ereignisse darstellen
müssen, da sonst die Multiplikationsregel der Wahrscheinlichkeit nicht
anwendbar ist. Wie RAWLS feststellt, ist es "klar, dass die Voten verschiedener
Personen nicht unabhängig sind. Da ihre Auffassungen durch den Verlauf der
Diskussion beeinflusst werden, sind die einfacheren Verfahren der
Wahrscheinlichkeits-Argumentation nicht anwendbar." [[23] RAWLS 1973, S.358.]
Weiterhin muss vorausgesetzt werden, dass es eine größere
Wahrscheinlichkeit für ein richtiges Urteil jedes Individuums gibt als für ein
falsches, denn im andern Fall wäre die Wahrscheinlichkeit größer, dass die
Minderheit recht hat. Diese Annahme kann bei schwierigen Fragestellungen wie der
nach dem Gesamtinteresse einer heterogenen Großgesellschaft in Bezug auf eine
anstehende Entscheidung nicht unbedingt {509} vorausgesetzt werden.
Die problematischste Bedingung für die Anwendbarkeit des
Wahrscheinlichkeitsarguments ist jedoch die, dass für alle Individuen die gleiche
Wahrscheinlichkeit besteht, die Frage nach dem Gesamtinteresse richtig zu
beantworten. Wenn man stattdessen von der schwer zu bestreitenden Annahme
ausgeht, dass die Erkenntnisfähigkeit der Individuen in dieser Hinsicht
Unterschiede aufweist, so erscheint nur der Schluss konsequent, die Urteile der
Individuen je nach ihrer Erkenntnisfähigkeit mit einem unterschiedlichen Gewicht zu versehen oder aber sogar die Bestimmung des Gesamtinteresses
völlig den dafür am besten geeigneten Individuen zu überlassen. "Ein
Antidemokrat könnte argumentieren, dass nur eine Minderheit hinreichend fähig
ist, den moralischen Imperativ unter dem verdunkelnden Schleier des
pragmatischen Eigeninteresses zu erkennen. ... Dementsprechend verlangt
PLATON,
dass eine kleine spezialisierte Gruppe von Wächtern die sozialen Entscheidungen
treffen soll. " [[24] ARROW 1963, S.86.]
Die Forderung nach einem zwar allgemeinen, aber nach dem
geistigen Vermögen abgestuften Stimmrecht hat zu seiner Zeit auch
J.St. MILL vertreten: "Zwar sollte jeder Stimmrecht besitzen, aber dass jeder gleiches
Stimmrecht besitzen sollte, ist eine völlig andere Aussage. ... Der weisere oder
bessere Mann hat Anrecht auf größeres Gewicht." [[25]
MILL 1969,
S.282.] Da RAWLS das
Mehrheitsprinzip ebenfalls in seiner selektiven Verwendung sieht, ist es nur
folgerichtig, dass er die {510} Argumentation von MILL als im Prinzip zulässig ansieht: "Von der Regierung wird angenommen, dass sie das Gemeinwohl anstrebt. ... In dem
Maße, wie diese Vermutung zutrifft und einige Menschen ausgemacht werden können, die überlegene Weisheit und Urteilskraft
haben, sind andere bereit, ihnen zu vertrauen und ihrer Meinung ein größeres
Gewicht zuzugestehen. ... Wenn man diese Voraussetzungen macht, kann ein
gewichtetes Stimmrecht völlig gerecht sein." [[26] RAWLS 1973, S.233.] Entsprechend besitzt für RAWLS "das Verfahren der Mehrheitsregel ... einen untergeordneten Platz als prozeduraler Mechanismus."
[[27] RAWLS 1973, S.356.]
Insgesamt bleibt bei RAWLS eigentlich unklar, warum das
Mehrheitsprinzip überhaupt Verwendung finden soll. Die Vorteile der kollektiven
Diskussion, die er anführt, können ja auch ohne Abstimmungsverfahren genutzt
werden, und um überhaupt zu einer Entscheidung zu kommen, gäbe es auch andere
Verfahren.
Auch in anderer Beziehung kommen diejenigen, die das
Mehrheitsprinzip in seiner selektiven Verwendung vertreten, in
Schwierigkeiten.
So können sie nur schwer föderale Entscheidungsstrukturen rechtfertigen, bei
denen nur von denjenigen abgestimmt wird, die von der anstehenden Entscheidung
vorwiegend betroffen sind. Außerdem muss bei der selektiven Auffassung des
Mehrheitsprinzips gefordert werden - so wie es ROUSSEAU noch konsequent getan
hat - , dass jede Form von Koalitionsbildungen unterbunden wird.
Bei der
selektiven Verwendung des Mehrheitsprinzips tritt mit aller Schärfe das Problem
{511} eigeninteressierter Abstimmungsstrategien auf. Während
bei einer aggregativen Verwendung des Mehrheitsprinzips eine eigeninteressierte Koalitionsbildung der
Individuen unproblematisch ist, da sie gerade dazu dient, die
Mehrheitsalternative durchzusetzen, [[28] RAWLS 1973, S.57.] muss bei der selektiven Verwendung des
Mehrheitsprinzips jede eigeninteressierte Abstimmungsstrategie von Individuen
und Gruppen die gesamte Konstruktion zerstören.
Es muss also vorausgesetzt
werden, dass die Individuen eine so hohe "staatsbürgerliche Moral" haben,
dass sie
auch dann für die im Gesamtinteresse liegende Alternative stimmen, wenn diese
ihrem individuellen Interesse völlig entgegengesetzt ist. Dass diese
Voraussetzung äußerst zweifelhaft ist, ist offensichtlich, vor allem wenn man
von geheimen Abstimmungen ausgeht, bei denen niemand gezwungen werden kann, sein
Abstimmungsverhalten zu begründen. Aus all diesen Gründen wird deutlich,
dass
zumindest die Praxis in parlamentarischen Systemen nicht als selektive
Verwendung des Mehrheitsprinzips interpretiert werden kann - was natürlich als
solches noch kein normativer Maßstab ist.
Zum Abschluss sei noch auf ein Problem hingewiesen, das nur
dann auftaucht, wenn man Abstimmungen nach dem Mehrheitsprinzip als Selektion
der richtigen Auffassung vom Gesamtinteresse interpretiert.
Man muss dann
nämlich immer annehmen, dass sich die Minderheit geirrt hat und mit ihrer
Auffassung vom Gesamtinteresse im Unrecht ist. Dies war auch die bereits
zitierte Auffassung von ROUSSEAU.
Andererseits stellt RAWLS jedoch richtig fest: "Während {512} die Bürger normalerweise ihr Verhalten der demokratischen
Autorität unterwerfen, d.h. den Ausgang einer Abstimmung als Setzung einer
verbindlichen Norm anerkennen, unterwerfen sie dieser nicht ihr Urteil." [[29]
RAWLS 1973, S.557.]
Die Minderheit kann jedoch eigentlich nur dann dabei
bleiben, dass ihre Auffassung vom Gemeinwohl richtig ist, wenn sie gleichzeitig
annimmt, dass sich die Mehrheit geirrt hat. Sie muss sich dann also jeweils der
Auffassung einer Mehrheit beugen, von der sie zugleich meint, dass sie falsch
ist. Dies wäre aber eine äußerst problematische Grundlage demokratischer
Loyalität gegenüber Mehrheitsentscheidungen.
Dies Problem taucht nicht auf, wenn man davon ausgeht, dass
die Individuen durch ihr Abstimmungsverhalten ihr individuelles Interesse
ausdrücken. Wenn dann zwei Individuen A und B auf die Frage: "Welche der zur
Entscheidung stehenden Alternativen ist am meisten in deinem Interesse?" eine
unterschiedliche Antwort geben, so bedeutet dies keineswegs, dass sich eines von
beiden geirrt haben muss, da ja die Interessen der beiden unterschiedlich sein
können. Beide Individuen können trotz unterschiedlicher Abstimmung "richtig"
abgestimmt haben. Für die Mitglieder der unterlegenen Minderheit bleibt
weiterhin diejenige Alternative, für die sie gestimmt haben, auch diejenige
Alternative, die ihrem individuellen Interesse am besten entspricht. Allerdings
kommt die siegreiche Mehrheitsalternative in der Regel dem Gesamtinteresse
näher. Es stellt dann keinerlei "demokratisches Paradox" dar, wenn die
unterlegene Minderheit einerseits gegen die Mehrheitsalternative gestimmt {513} hat und wenn sie andererseits aus demokratischer
Überzeugung zugleich will, dass die Mehrheitsalternative realisiert wird. [[30]
Ein solches Paradox sieht z. B. WOLLHEIM 1962.]
Bei der Abstimmung geht es um diejenige Alternative, die im
individuellen Interesse der Individuen ist, während es bei der kollektiven
Entscheidung um diejenige Alternative geht, die nach
Aggregation dieser individuellen Interessen diejenige Alternative
ist, die dem Gesamtinteresse am besten entspricht. Die Tatsache, dass
die Mehrheit der Individuen aufgrund ihrer anderen Interessenlage anders
gestimmt hat, ist für die Mitglieder der Minderheit nicht der geringste Anlass,
an der Richtigkeit ihrer eigenen Abstimmung zu zweifeln. Sie würden in genau der
gleichen Weise wieder abstimmen, wenn sie noch einmal vor dieselbe Entscheidung
gestellt würden. "Falsch" kann ein Individuum hier nur dann abstimmen, wenn es
entgegen seinen eigenen Interessen abgestimmt hat.
Während bei der aggregativen Verwendung des Mehrheitsprinzip ein Individuum
also nur aus "Dummheit" falsch abstimmen kann, kann ein Individuum bei der
selektiven Verwendung des Mehrheitsprinzips auch aus "Unmoral" und "Eigennutz"
falsch abstimmen, insofern es sich dabei anstatt vom Gesamtinteresse von seinem
Eigeninteresse leiten lässt. Damit stellt sich aber auch das Toleranzproblem
gegenüber derartigen abweichenden Meinungen verschärft.
{514}
18. Kapitel
Die Mehrheitsalternative
§ 110 Das Mehrheitsprinzip und die Bestimmung der
Mehrheitsalternative
Die Anwendung des Mehrheitsprinzips bedeutet, dass diejenige Alternative als kollektiv gewählt gilt, die gegenüber jeder andern Alternative von einer Mehrheit der Individuen vorgezogen wird. Diese Alternative, die im Paarvergleich jeder andern Alternative nach der Zahl der befürwortenden Individuen überlegen ist, wird von BLACK als Mehrheitsalternative bezeichnet. [[1] Siehe BLACK 1971, S.57.] Diese Fassung des Mehrheitsprinzips wurde zuerst von CONDORCET vorgeschlagen, weshalb man auch vom CONDORCET-Kriterium spricht.
Das Mehrheitsprinzip baut auf den Rangfolgen der Alternativen für die einzelnen Individuen gemäß ihren Interessen auf. Wenn alle Individuen die zur Entscheidung anstehenden Alternativen in eine vollständige, transitive Rangordnung gebracht haben, so lässt sich aus der Aggregation dieser Präferenzrangfolgen die Mehrheitsalternative bestimmen, sofern eine solche existiert. [[2] Zum Fehlen einer Mehrheitsalternative s. u. § 135. Eine Rangordnung ist transitiv, wenn gilt: Wenn x > y und y > z, dann gilt auch x > z.]
Das Mehrheitsprinzip baut also nur auf einer ordinalen Bestimmung der individuellen Nutzen auf. Diejenige Alternative, die in den Präferenzrangfolgen der Individuen im Vergleich zu jeder andern {515} Alternative häufiger vor als hinter dieser auftritt, ist die Mehrheitsalternative.
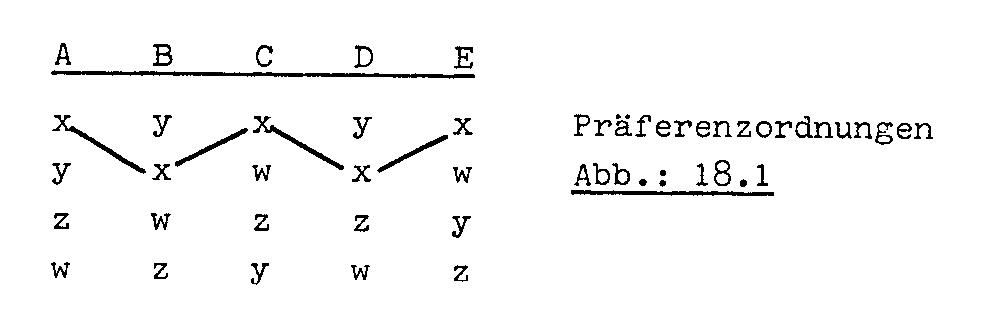
Dies kann an einem Beispiel veranschaulicht werden, bei dem die fünf Individuen A, B, C, D und E nach dem Mehrheitsprinzip über die vier Alternativen w, x, y und z entscheiden. Ihre Interessen in Bezug auf diese Entscheidung lassen sich durch die folgenden Präferenzordnungen wiedergeben, wobei die Alternativen gemäß ihrer nutzenmäßigen Rangfolge unter dem jeweiligen Individuum angeordnet sind: [[3] Zum Zwecke der Vereinfachung wird vorausgesetzt, dass die Individuen nur "starke" Präferenzordnungen aufstellen, bei denen also keine Indifferenz zwischen Alternativen vorkommt.]

Wie man aus der Tabelle ersieht, ist in diesem Fall die
Alternative x die Mehrheitsalternative. Dies lässt sich anhand der
Präferenzordnungen relativ leicht feststellen. Um zu prüfen, ob eine bestimmte
Alternative die Mehrheitsalternative ist, zieht man einen Linienzug durch diese
Alternative, wie in der Abb. 18.1 durch die Alternative x. Es handelt sich bei x
dann um die Mehrheitsalternative, wenn keine andere Alternative häufiger
oberhalb dieses Linienzuges zu finden ist als unterhalb dieses Linienzuges. Denn
wenn eine andere Alternative wie z. B. y bei Individuum B oberhalb des
Linienzuges durch x zu finden ist, so heißt dies, dass B die Alternative {516} y gegenüber x vorzieht; wenn dagegen y unterhalb des
Linienzuges durch x steht, wie z. B. bei Individuum A, so wird x gegenüber y
vorgezogen.
Man kann das Mehrheitsprinzip auch anhand einer
sogenannten Wahlmatrix verdeutlichen.[[4] Siehe BLACK 1971, S.35ff.] Die Wahlmatrix vergleicht jede
Alternative mit jeder anderen und gibt an, wie viele Individuen gemäß ihrer
Interessenlage die eine Alternative gegenüber der anderen vorziehen. Dazu bildet
man eine Tabelle, bei der man sämtliche Alternativen einmal am linken Rand und
einmal am oberen Rand einträgt. In die einzelnen Felder lassen
sich dann die Ergebnisse des paarweisen Vergleichs eintragen, wobei die vordere
Zahl die Befürworterzahl der links stehenden Zeilen-Alternative angibt, während
die hintere Zahl die Befürworterzahl der oben stehenden Spalten-Alternative
angibt. Für die Präferenzordnungen aus Abb. 18.1 würde sich folgende Wahlmatrix
ergeben:
Wahlmatrix zu Abb. 18.1
| w | x | y | z | |
| w | - | 0:5 | 2:3 | 3:2 |
| x | 5:0 | - | 3:2 | 5:0 |
| y | 3:2 | 2:3 | - | 4:1 |
| z | 2:3 | 0:5 | 1:4 | - |
Abb. 18.2
Aus der Wahlmatrix ist z. B. zu entnehmen, dass eine
aufrichtige Abstimmung zwischen y und x mit 2:3 Stimmen gegen y ausgehen würde.
Dies entspricht den Präferenzordnungen, denen gemäß bei den 2 Individuen B
und D y vor x rangiert, während bei den 3 Individuen A, C und E x vor y
rangiert. Die Mehrheitsalternative {517}
lässt sich jetzt dadurch
finden, dass man die Zeilen danach durchgeht, ob eine Alternative alle anderen
geschlagen hat. In unserm Beispiel wäre x die Mehrheitsalternative, denn x ist
in paarweiser Abstimmung gemäß den tatsächlichen Präferenzen der Individuen
jeder andern Alternative stimmenzahimäßig überlegen.
Falls Individuen zwischen zwei Alternativen indifferent
sind, sodass sich schwache Präferenzordnungen ergeben, so bedeutet dies kein
Problem, denn diese Individuen können unberücksichtigt gelassen werden. Wenn
jemand sich der Stimme enthält, so hat dies keinen Einfluss zugunsten einer der
beiden Alternativen. [[5] Siehe dazu auch DAHL 1970, S.39.]
Man kann das Mehrheitsprinzip auch mit schwachen
Präferenzordnungen definieren. So versteht ARROW unter dem Mehrheitsprinzip
diejenige Entscheidungs-Regel, bei der für das Kollektiv die Alternative x dann
besser oder gleichwertig im Verhältnis zur Alternative y ist, wenn die Zahl der
Individuen, für die x besser oder gleichwertig gegenüber y ist, mindestens so
groß ist wie die Zahl derer, für die y besser oder gleichwertig gegenüber x
ist. [[6] Vgl. ARROW 1963, S.46. Siehe auch die analoge
Formalisierung bei SEN 1970, S.71.]
Wie SEN bemerkt, sind die Formulierungen mithilfe der starken und der
schwachen Präferenzrelation äquivalent, da die indifferenten Individuen immer
beiden Alternativen gleichmäßig hinzugezählt werden. In der Formulierung von ARROW besteht allerdings insofern ein Unterschied zur obigen Formulierung, als
bei ARROW im Falle von Stimmengleichheit beide Alternativen als kollektiv
gleichwertig angesehen werden. Nach der {518} hier verwendeten Formulierung des Mehrheitsprinzips
handelt es sich in diesem Fall jedoch nicht um die Mehrheitsalternative, denn
diese muss jeder andern Alternative stimmenzahlmäßig überlegen sein. Dies
bedeutet zugleich, dass es höchstens eine Mehrheitsalternative geben kann.
[[7] Siehe BLACK 1971, S.14.]
§ 111 Eingipfligkeit der individuellen Präferenzen, Mehrheitsalternative und mediane Spitzenalternative
Die Mehrheitsalternative hat einige besondere
Eigenschaften, die im Folgenden näher dargestellt werden sollen. So besteht ein
besonderer Zusammenhang zwischen der Mehrheitsalternative, die allen andern
Alternativen im Paarvergleich stimmenzahlmäßig überlegen ist, und derjenigen
Alternative, die von dem seiner Interessenlage nach "mittleren" bzw. medianen
Individuum bevorzugt wird. Beide fallen unter bestimmten Umständen zusammen, was
am folgenden Beispiel demonstriert werden soll.
Angenommen ein Kollektiv von 5 Individuen A, B, C, D und E
hat nach dem Mehrheitsprinzip darüber zu entscheiden, wie hoch die Benzinsteuer
sein soll. Es sollen 7 Alternativen existieren: 0, 10, 20, 30, 40, 50 und 60
Pfennig pro Liter. Dabei bestehen die folgenden Präferenzordnungen der
Individuen: {519}

Die Präferenzordnung eines Individuums kann man auch durch
den Kurvenzug in einem Koordinaten-System veranschaulichen, bei dem auf der
horizontalen Achse die Alternativen eingetragen werden, während auf der
vertikalen Achse die dazugehörigen ordinalen Nutzen abgetragen werden. Die obige
Präferenzordnung des Individuums C sähe dann folgendermaßen aus:
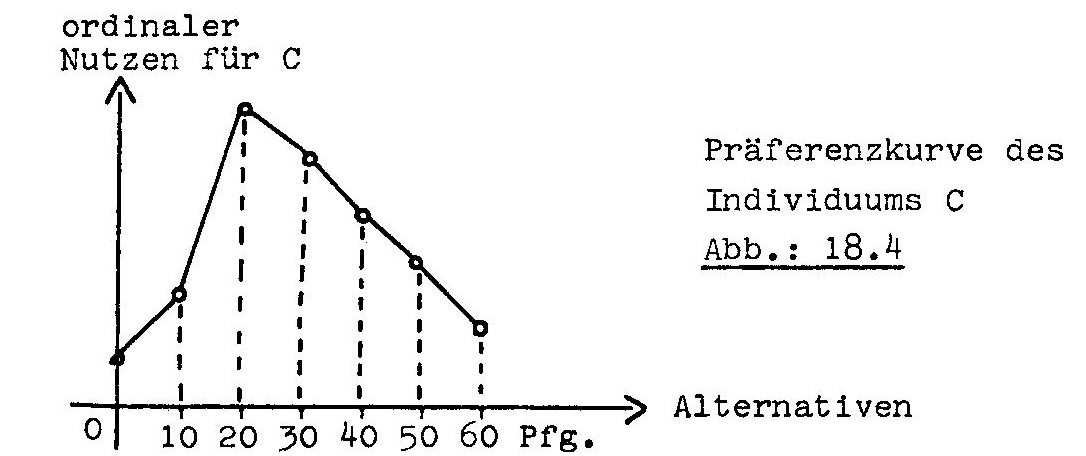
Dabei sind die individuellen Nutzenwerte für die
Alternativen zur besseren Anschaulichkeit durch eine Linie verbunden, sodass sich
eine Präferenzkurve ergibt. [[8] Die Darstellungsform stammt von BLACK 1971, S.5ff.] Da diese Präferenzkurve aufgrund interpersonal
nicht vergleichbarer, nur ordinaler Nutzenwerte gewonnen wurde, spielt nur die
relative Höhe {520}der Kurve im Verhältnis zu andern Punkten derselben Kurve
eine Rolle. Wenn die Kurve also bei der einen Alternative höher verläuft als bei
einer andern Alternative, so bedeutet dies, dass die erste Alternative einen
höheren Platz in der nutzenmäßigen Rangordnung des betreffenden Individuums
besitzt. Die absolute Höhe spielt dabei keine Rolle, d.h. man könnte die Kurve
auch ohne Veränderung ihres Informationsgehaltes in der Höhe zusammendrücken
oder auseinanderziehen, sofern nur die relative Höhe der Kurve an den
Alternativen gleich bleibt. Außerdem kann man natürlich die Höhe der Kurve
verschiedener Individuen nicht miteinander vergleichen, da es sich um eine
interpersonal nicht vergleichbare Nutzenmessung handelt.
Wenn man nun die Präferenzordnungen aller 5 Individuen aus
Abb.18.3 in dasselbe Koordinaten-System einzeichnet, so ergibt sich folgendes
Bild:
Präferenzkurven aller Individuen aus 18.3.
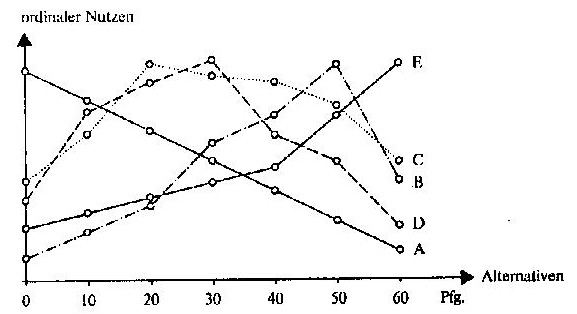
Abb. 18.5
Wie man aus Abb. 18.5 ersieht, haben die Präferenzkurven
aller Individuen in diesem Beispiel nur einen Gipfelpunkt, von dem aus sie nach
einer oder nach beiden Seiten hin immer mehr abfallen. Die individuellen
Präferenzen sind also so beschaffen, dass für jedes Individuum ein bestimmter
Steuersatz {521} die Spitzenalternative bildet und dass die übrigen
Alternativen von den Individuen als umso schlechter angesehen werden, je weiter
sie auf der horizontalen Achse von der Spitzenalternative, dem individuellen
Optimum, entfernt liegen. [[9] Dabei sind allerdings immer nur Entfernungen auf
derselben Seite miteinander vergleichbar.] Wenn sich die Alternativen auf der horizontalen Achse
derartig anordnen lassen, dass man darüber für alle Individuen entsprechend
geformte Präferenzkurven einzeichnen lassen, so spricht man von "eingipfligen
Präferenzen" (single-peaked preferences). [[10] Siehe dazu BLACK 1948 und 1971.]
Dabei ist es wichtig festzuhalten,
dass es nur irgendeine Anordnung der Alternativen auf der horizontalen Achse
geben muss, bei der sämtliche individuellen Präferenzkurven eingipflig werden.
Es muss sich also nicht unbedingt um eine größenmäßige Anordnung der Alternativen
handeln wie in unserm Beispiel, wo die Alternativen entsprechend der Höhe des
Steuersatzes geordnet sind. [[11] Siehe BLACK 1971, S.7.]
Wenn sich die Präferenzen aller Individuen durch derartige
eingipflige Präferenzkurven wiedergeben lassen, so bedeutet dies, dass den
Präferenzen aller Individuen irgendeine gemeinsame Dimension zugrunde
liegt. In unserm Beispiel besteht diese Dimension gewissermaßen in der
Einstellung zum Autoverkehr. Am positivsten ist Individuum A dazu eingestellt,
das am liebsten überhaupt keine Benzinsteuer hätte und für das eine Entscheidung
umso schlechter ist, je höher die Steuer ist. Dann kämen {522} nacheinander die Individuen C, D und B, die jeweils
wachsende Steueranteile befürworten, bis hin zum Motorisierungsgegner E, der
nach dem Motto urteilt: "Je höher die Benzinsteuer, desto besser für mich!".
Wie ARROW ausführt, existiert z. B. im politischen Bewusstsein eine gemeinsame
Dimension in Form einer Rechts-Links-Anordnung der Parteien, zumindest in der
europäischen Parteienstruktur der Vorkriegszeit. "Individuen mochten zu
irgendeiner der Parteien gehören; doch jedes anerkannte die gleiche Anordnung in
dem Sinne, dass es von zwei Parteien links von seiner eigenen das Programm der
weniger linken vorzog, und entsprechend war es mit Parteien auf der Rechten."
[[12] ARROW 1963, S.76.]
Wenn die Präferenzen der Individuen in der beschriebenen
Weise eingipflig sind, so besitzt das seiner Interessenlage nach "mittlere"
Individuum, dessen Spitzenalternative den Medianwert aller Spitzenalternativen
bildet, eine besondere Stellung. [[13] Den Medianwert erhält man, indem man die Einzelwerte der
Größe nach ordnet und dann den "mittleren" Wert heraussucht, zu dem es genau soviel größere wie kleinere Einzelwerte gibt. Für die Werte 1, 2, 3, 4, 10,
100 und 1000 ist der Median z. B. "4".] In unserem Beispiel ist das Individuum D
seiner Interessenlage nach in der Mitte, seine Spitzenalternative "30 Pfg." ist
die mittlere aller Spitzenalternativen und bildet den mittleren Gipfel in Abb.
18.5.
Das besondere an diesem Medianwert der Spitzenalternativen besteht nun darin, dass es sich hierbei immer um die
Mehrheitsalternative handelt. [[14] Zum Beweis s. BLACK 1971, S.16ff. sowie ARROW 1963,
S.77ff. Da bei gerader Stimmenzahl kein eindeutiger Medianwert existiert, gilt
dieser Beweis nur bei einer ungeraden Anzahl von Individuen.] Bei eingipfligen Präferenzen
{523} der Individuen bekommt die mediane Spitzenalternative im
Paarvergleich gegenüber jeder andern Alternative eine Stimmenmehrheit.
Damit ist übrigens zugleich nachgewiesen, dass im Falle
eingipfliger Präferenzen und ungerader Anzahl der Individuen immer eine
Mehrheitsalternative existiert und keine zyklischen Mehrheiten vorkommen, bei
denen etwa x mehr Stimmen bekommt als y, y mehr Stimmen als z, aber z
wiederum mehr Stimmen als x. [[15] Zum Problem zyklischer Mehrheiten s.u. § 136.] Bei ARROWs 'Allgemeinem Möglichkeits-Theorem' war
eine der Bedingungen die, dass alle logisch möglichen Präferenzordnungen zugelassen
sein müssen. Dies war die Bedingung des "unbeschränkten Bereichs" der
Präferenzen. BLACK hat nun nachgewiesen, dass transitive individuelle
Präferenzordnungen immer dann durch das Mehrheitsprinzip zu einer transitiven
kollektiven Präferenzordnung aggregiert werden, wenn die individuellen
Präferenzen eingipflig sind. [[16] Siehe hierzu auch die weiterführende Diskussion und die
Literaturhinweise bei SEN 1970, S.166ff.]
Dass im obigen Beispiel der Medianwert der Spitzenalternativen, die von Individuum D bevorzugte Alternative "30 Pfg.", tatsächlich die Mehrheitsalternative darstellt, kann man anhand der Präferenzordnungen leicht erkennen. Wenn man in Abb.18.3 die Alternative "30 Pfg." bei allen Individuen durch einen Linienzug verbindet, so tauchen alle andern Alternativen nur höchstens zweimal oberhalb dieses Linienzuges auf, sodass die Alternative "30 Pfg." mit 3 von 5 Stimmen immer eine Mehrheit erhält. {524}
Dass das Mehrheitsprinzip den Medianwert der individuellen Spitzenalternativen auswählt und nicht etwa das arithmetische Mittel, hängt damit zusammen, dass das Mehrheitsprinzip nicht auf kardinalen Nutzenmessungen basiert, sondern nur auf Präferenzordnungen, also ordinalen nutzenmäßigen Rangfolgen. An den Eigenschaften des Medianwertes kann dabei veranschaulicht werden, inwiefern sich die Nichtberücksichtigung von Präferenzintensitäten bzw. kardinalen Nutzendifferenzen durch das reine Mehrheitsprinzip problematisch auf das Ergebnis dieses kollektiven Entscheidungsverfahrens auswirkt. [[17] Siehe dazu ausführlich unten § 138.]
Im Gegensatz zum arithmetischen Mittel ist nämlich der
Median unempfindlich gegenüber allen Veränderungen der Einzelwerte, sofern nur
der Medianwert selbst seine Mittelposition behält und nicht verändert wird.
Selbst wenn also in unserm Beispiel die Individuen B, C und E ihre Auffassung
über die für sie beste Benzinsteuer drastisch senken würden, so bliebe der
Medianwert "30 Pfg." unter Umständen unverändert. Wenn die Spitzenalternativen
der Individuen jetzt folgendermaßen lauten würden (die alten Werte stehen in
Klammern): A = 0 (0); B = 30 (50); C = 0 (20); D = 30 (30) und E = 30 (60), so
ergäbe sich in der Reihe: 0, 0, 30, 30, 30 immer noch derselbe Medianwert "30".
Trotz teilweise stark gesenkter Präferenzen hinsichtlich des individuell besten
Steueranteils würde also die Mehrheitsentscheidung weiterhin 30 Pfg. betragen.
Im Unterschied zum unverändert gebliebenen Medianwert hätte sich das
arithmetische Mittel aufgrund solcher Veränderungen der Einzelwerte erheblich {525} verändert, denn es wäre von 33,33 Pfg. auf 22 Pfg.
gesunken.
An dieser Unempfindlichkeit des Medians gegenüber
Veränderungen der Einzelwerte wird deutlich, dass das Mehrheitsprinzip keine
Präferenzintensitäten bzw. Nutzendifferenzen sondern nur Rangordnungen in Bezug
auf die Alternativen erfasst.
Um die Problematik zu veranschaulichen, sollen
einmal - allerdings stark vereinfachte - kardinale Nutzenfunktionen angenommen
werden. Der Nutzen der Spitzenalternativen im Verhältnis zum Status quo soll für
alle Individuen gleich sein, und pro Pfennig Differenz zur individuellen
Spitzenalternative soll der Nutzen einer Alternative um eine Einheit sinken.
Wenn man diese Nutzenfunktionen in einem entsprechenden Koordinaten-System
aufzeichnen würde, so hätten alle Kurven die gleiche Gipfelhöhe bei der
individuellen Spitzenalternative und würden nach den Seiten im Winkel von 45
Grad gradlinig abfallen. Die Gesamtnutzenkurve würde man dann durch eine
Addition der individuellen Nutzenkurven erhalten. Der Gipfel dieser
Gesamtnutzenkurve liegt dann über derjenigen Alternative, bei der der
Gesamtnutzen sein Maximum erreicht. [[18] Zum interpersonal vergleichbaren, kardinalen
Nutzenbegriff s. o. die §§ 38 und 39.]
Wenn die individuellen Nutzenfunktionen
derartig beschaffen sind, so ist der Gesamtnutzen einer Alternative umso höher,
je geringer die geldmäßige Gesamtdifferenz zwischen dieser Alternative und allen
individuellen Spitzenalternativen ist. Da das arithmetische Mittel derjenige
Wert ist, bei dem die Differenz zu den Einzelwerten minimiert wird, ist in
diesem Fall das arithmetische Mittel aller Spitzenalternativen diejenige {526} Alternative mit dem höchsten Gesamtnutzen und nicht der
Medianwert.
Andererseits hat der Median aber den in der
Abstimmungspraxis äußerst wichtigen Vorteil, dass er relativ unempfindlich ist
gegenüber Übertreibungen und bewusst verzerrte Präferenzäußerungen der
Individuen.
Wenn z. B. Individuum C, das eigentlich einen Steueranteil von 20 Pfg. pro Liter bevorzugt, die kollektive Entscheidung dadurch zu drücken
versucht, dass es statt der 20 Pfg. nur einen Steueranteil von 0 Pfg. als seine
Spitzenalternative angibt, so hätte dies bei Anwendung des Mehrheitsprinzips
keinerlei Auswirkungen auf das Ergebnis, denn der Median und damit die
Mehrheitsalternative bleibt unverändert bei 30 Pfg.
Dieses Argument für den Medianwert und gegen das
arithmetische Mittel wurde bereits 1907 von dem Statistiker GALTON vorgetragen,
der die Frage stellte, wie man aufgrund der individuellen Schätzwerte z. B. in
Bezug auf die Höhe kollektiver Ausgaben für einen bestimmten Zweck zu einer
vernünftigen kollektiven Entscheidung kommen könne. "Diese Entscheidung besteht
sicherlich nicht im Durchschnittswert aller Schätzwerte, wodurch
'Sonderlingen' eine Abstimmungsmacht im Verhältnis zu ihrer Sonderlichkeit verliehen würde. Ein unsinnig
großer oder kleiner Schätzwert würde am Ergebnis einen größeren Eindruck
hinterlassen als ein Schätzwert von vernünftiger Größe, und je mehr ein
Schätzwert von der Masse der übrigen abweicht, umso größeren Einfluss würde er
ausüben. Ich möchte aufzeigen, dass der mittelste Schätzwert derjenige ist, gegen
den die wenigsten Einwände erhoben werden können, bei dem die Stimmenzahl dafür,
dass er zu hoch sei, genau ausgeglichen wird durch die Stimmenzahl {527} dafür, dass er zu niedrig sei. Jeder andere Wert wird von
einer Mehrheit der Abstimmenden als entweder zu hoch oder zu niedrig
verworfen." [[19] GALTON in BLACK 1971, S.188.] {528}
19. Kapitel
Verschiedene Abstimmungsverfahren und die Auswirkungen von
Koalitionsbildung
§ 112 Entscheidungs-Regel und konkretes
Entscheidungsverfahren
An dieser Stelle erscheint es sinnvoll, den Unterschied
zwischen den bloßen Entscheidungsregeln und realen Entscheidungsverfahren zu
betonen. Das Mehrheitsprinzip als solches stellt ja nur eine logische Aggregations-Regel für die individuellen Präferenzrangfolgen dar. Damit ist es
jedoch noch kein konkretes Entscheidungsverfahren, denn dazu müsste u. a. erst
geregelt werden, wie die individuellen Präferenzrangfolgen und die Alternativen
bestimmt werden. Erst dann geht die logische Aggregations-Regel in eine konkrete
Institution über.
Wenn z. B. nach Art individualistischer Entscheidungs-Systeme
die Formulierung der individuellen Präferenzen den betreffenden Individuen
selber überlassen bleibt, so können die Individuen ihre Interessen im Rahmen der
gesetzten institutionellen Regelungen autonom verfolgen. Sie können dann auch
ihr Abstimmungsverhalten aufgrund von strategischen Überlegungen und Absprachen
mit andern so gestalten, wie es ihrem Eigeninteresse am besten entspricht. In
diesem Fall muss das Abstimmungsverhalten eines Individuums nicht notwendig mit
den eigentlichen Präferenzen in Bezug auf die anstehende Entscheidung
übereinstimmen, denn es kann z. B. manchmal vorteilhaft sein, nicht {529} für die eigene Spitzenalternative zu stimmen, da sie ohne
Aussicht auf Erfolg ist.
Weil in einem solchen Fall die angewandte
Entscheidungs-Regel selber einen Einfluss auf die ausgedrückten Präferenzen hat,
ist dabei die institutionelle Umsetzung einer Entscheidungs-Regel in ein
konkretes Entscheidungsverfahren nicht nur eine Operationalisierung sondern
zugleich eine Modifizierung der eigentlichen Entscheidungs-Regel. Um diesen
Unterschied zu verdeutlichen, erscheint es sinnvoll, ein reales Verfahren nach
dem Mehrheitsprinzip, das auf einer autonomen Stimmabgabe der Individuen
beruht, als Mehrheitssystem zu bezeichnen.
In einem solchen
Mehrheitssystem wird das Mehrheitsprinzip also nicht auf die tatsächlichen
Präferenzen der Individuen zu den anstehenden Alternativen angewandt, sondern
auf Präferenzäußerungen, denen u. U. eigeninteressierte Strategien und Absprachen
zugrunde liegen. [[1] In dieser Differenz zwischen logischer
Entscheidungsregel und konkretem Entscheidungsverfahren liegt übrigens auch
ein Grund für die begrenzte Relevanz einer rein logischen Analyse. Vgl. auch die
Überlegungen zu Theorie und Praxis bei SEN 1970, S.187ff.]
In den konkreten Entscheidungsverfahren treten dann auch
Informationsprobleme, Ungewissheit und sonstige Entscheidungskosten auf, die
einen Einfluss auf das Abstimmungsverhalten der Individuen haben können und nicht
unerheblich für die Frage nach der praktischen Anwendbarkeit eines Entscheidungsverfahrens sind.
§ 113 Die Regel der relativen Mehrheit bei einmaliger Abstimmung
Entsprechend dem oben definierten Mehrheitsprinzip {530} müssen eigentlich alle Alternativen paarweise miteinander
verglichen werden, um die Mehrheitsalternative zu bestimmen. Der Aufwand für
die Durchführung eines solchen Entscheidungsverfahrens steigt mit der Zahl der
Alternativen jedoch sehr rasch an, weil sich die Zahl möglicher
Paarkombinationen sprunghaft erhöht. Während bei 2 Alternativen nur 1
Paarvergleich notwendig ist, sind bei 3 Alternativen 3 Paarvergleiche notwendig
und bei 10 Alternativen sind es bereits 45 mögliche Paarkombinationen.
Zwar müsste man diese Paarvergleiche nicht in einzelnen Abstimmungen durchführen,
sondern könnte sie auch aufgrund der vollständigen Präferenz-Rangfolgen der
Individuen ermitteln, aber trotzdem bliebe das Verfahren noch recht umständlich
und ließe sich dann auch nicht durch bloßes Handaufheben durchführen. [[2] Zum Verfahren der paarweisen Abstimmung s.u. § 119.] Aus diesem Grund wird das Mehrheitsprinzip meist derart
praktiziert, dass alle Alternativen gemeinsam zur Abstimmung
gestellt werden und dann diejenige Alternative als kollektiv gewählt gilt, die
die meisten Stimmen bekommen hat. Ein solches
Verfahren kann als relative Mehrheitsregel bezeichnet werden.
[[3] BLACK nennt die relative Mehrheitsregel "einmalige
Abstimmung" (single vote). S. dazu BLACK 1971, S.67ff.]
Die Durchführung eines derartigen Verfahrens ist recht einfach, denn es bedarf
nur einer einzigen Abstimmung und einer Auszählung der Stimmen für die {531} verschiedenen Alternativen.
Ein Problem der relativen Mehrheitsregel besteht
darin, dass u. U. mehrere Alternativen gleichzeitig die höchste Stimmenzahl
erhalten können, sodass die kollektive Entscheidung nicht eindeutig ist. Es
müssen für diesen Fall also zusätzliche Regelungen eingeführt werden. Eine
Möglichkeit hierfür wäre etwa eine weitere Abstimmung nur zwischen den
Alternativen mit der höchsten Stimmenzahl nach Art eines Stichentscheids. [[4]
Zum Problem der Stimmengleichheit s. a. DAHL 1970, S.39ff.
Wie jedoch unten gezeigt wird, kann Stimmengleichheit bei eigeninteressierter
Koalitionsbildung nur auftreten, wenn keine Mehrheitsalternative vorhanden ist.]
Ein gewichtigeres Problem der relativen Mehrheitsregel
besteht darin, dass bei "aufrichtiger" Abstimmung der Individuen für
ihre Spitzenalternative u. U. eine Alternative mit einem relativ geringen
Stimmenanteil - gemessen an der Gesamtzahl der Abstimmenden - erfolgreich sein kann.
Diese Möglichkeit besteht vor allem dann, wenn sehr viele Alternativen zur
Entscheidung stehen, sodass sich die Stimmen stark aufsplittern können.
Wenn z. B.
100 Individuen über 5 Alternativen abstimmen, so reichen bereits 21 Stimmen
für eine Alternative zur relativen Mehrheit, wenn sich die 100 Stimmen nach dem
Schema 21 : 20 : 20 : 20 : 19 aufteilen. Wenn auch noch Enthaltungen vorliegen,
kann der erforderliche Prozentsatz noch niedriger sinken. Damit tritt das
Problem der Nicht-Berücksichtigung von Präferenzintensitäten mit
voller Schärfe auf, weil jetzt sogar ein geringer Anteil der Individuen mit
schwachen Präferenzintensitäten den Ausschlag geben kann.
{532}
Wenn jedes Individuum bei der Abstimmung ohne strategische
Überlegungen starr für seine Spitzenalternative stimmt, so ergeben sich zwischen
der relativen Mehrheitsregel und dem oben definierten Mehrheitsprinzip
erhebliche Differenzen, wie BLACK am Beispiel einer Auswahl aus mehreren
Kandidaten zeigt. "Der Effekt der einmaligen Abstimmung (nach der relativen
Mehrheitsregel, E.W.) besteht darin, die Kenntnis aller Präferenzen (des
Wählers, E.W.) zu unterdrücken, ausgenommen seine oberste Präferenz für einen
bestimmten Kandidaten; abgesehen davon muss er alle Kandidaten auf dem gleichen
Niveau einstufen. ... Wenn der Wähler zwischen zwei oder mehr Kandidaten
indifferent ist, von denen er jeden gegenüber irgendeinem von den übrigen
vorzieht, so fälscht die einmalige Abstimmung sogar seine Präferenzordnung in
Bezug auf den Ausdruck seiner obersten Präferenz." [[5] BLACK 1971, S.68. Diese Schwäche der relativen
Mehrheitsregel war bereits von BORDA und CONDORCET festgestellt worden. S.
BLACK 1971, S.157 u. 166.]
Nur in dem außergewöhnlichen Fall, dass jedes Individuum nur eine Spitzenalternative hat und gegenüber allen anderen Alternativen indifferent ist, ergibt sich bei "aufrichtiger" Abstimmung aller Individuen nach der relativen Mehrheitsregel dieselbe Entscheidung wie beim Mehrheitsprinzip, und die Mehrheitsalternative setzt sich durch. "Aber diese Einschränkung in Bezug auf die Form der Präferenzkurve ist von extremer Strenge; und diese wie auch andere Kurvenformen, die die Wahl der Mehrheitsalternative bei einmaliger Abstimmung zur Folge hätten, können in der Praxis kaum vorkommen." [[6]BLACK 1971, S.68.] {533}
§ 114 Eigeninteressierte Koalitionsbildung im relativen Mehrheitssystem
Angesichts dieser schweren Einwände mag es erstaunlich
sein, dass die relative Mehrheitsregel in der Abstimmungspraxis so häufig
Verwendung findet. Die Antwort hierauf ist relativ einfach und verblüffend: Wenn
alle Individuen die für sie vorteilhaftesten Abstimmungskoalitionen eingehen,
führt die relative Mehrheitsregel ebenfalls dazu, dass eine vorhandene
Mehrheitsalternative gewählt wird. [[7] Da BLACK ähnlich wie seine Vorgänger nur "aufrichtiges",
nicht-strategisches Abstimmungsverhalten untersucht, konnte er diese Konvergenz
der Verfahren nicht feststellen.]
Dies für die Praktizierung des Mehrheitsprinzips äußerst wichtige Ergebnis soll
im Folgenden an einem Beispiel demonstriert werden, bei dem 7 Individuen A bis G
über 7 Alternativen t bis z nach der relativen Mehrheitsregel abstimmen.
Präferenzordnungen
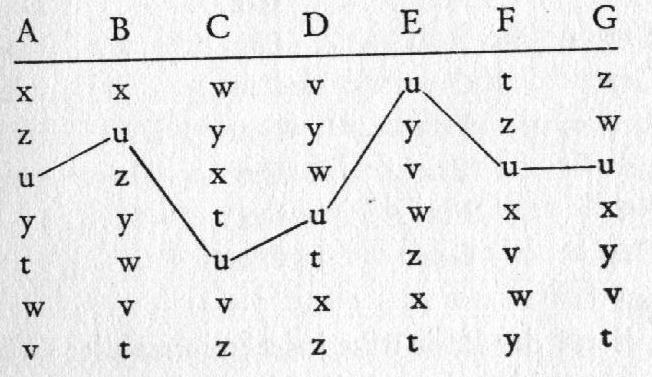
Abb.19.1
Anhand dieser Präferenzordnungen der Individuen soll nun
demonstriert werden, dass bei eigeninteressierter Koalitionsbildung auch im
relativen Mehrheitssystem eine vorhandene Mehrheitsalternative gewählt wird.
Eine Koalition K mit der Abstimmungsvereinbarung x ist
dabei dann für die beteiligten Individuen am vorteilhaftesten, {534} wenn es keine andere Gewinnkoalition gibt,
die ein Ergebnis durchsetzen kann, das für mindestens ein Mitglied der Koalition
K besser ist als x.
Angenommen im Beispiel aus Abb. 19.1 hätte jedes Individuum
die Absicht, "aufrichtig" für seine Spitzenalternative zu stimmen (s. Abb. 19.2,
1. Abstimmung).
Dies würde bedeuten, dass die Alternative x gewählt wird, denn
sie hat mit zwei Stimmen die relative Mehrheit, da alle anderen Alternativen nur
eine Stimme erhalten.
In diesem Fall wären zumindest die Individuen C, D und E
nicht die für sie vorteilhafteste Abstimmungskoalition eingegangen, denn hätten
sie untereinander vereinbart, für y zu stimmen, so wäre y realisiert worden,
eine Alternative, die alle 3 gegenüber x vorziehen, wie man aus ihren
Präferenzordnungen ersehen kann.
Die Konsequenz aus dieser strategischen
Überlegung drückt sich in der 2. Abstimmung in Abb. 19.2 aus. Jetzt erhält y die
relative Mehrheit der Stimmen mit 3 Stimmen.
In diesem Fall hätten jedoch die übrigen 4 Individuen A, B,
F und G nicht die für sie vorteilhafteste Abstimmungsvereinbarung getroffen,
denn wenn sie alle geschlossen für z stimmen würden, so könnten sie z anstelle
von y mit relativer Mehrheit durchsetzen, und für alle vier Individuen ist z
besser als y. (S. Abb. 19.2, 3. Abstimmung). Mit 4 von 7 Stimmen hätten sie in
diesem Fall sogar die absolute Mehrheit der Stimmen.
Trotzdem wäre dies noch
nicht die für alle Mitglieder der Koalition vorteilhafteste Koalition. Der
schwache Punkt dieser Koalition auf der Basis z ist das Individuum B, für das es
noch eine Gewinnkoalition mit einem besseren Ergebnis als {535} z gibt.
Wenn nämlich die Individuen B, C, D und E
geschlossen für die Alternative u stimmen, so bedeutet dies für alle Mitglieder
der Koalition gegenüber der Alternative z eine Verbesserung (s. Abb. 19.2, 4.
Abstimmung).
Koalitionsentwicklung
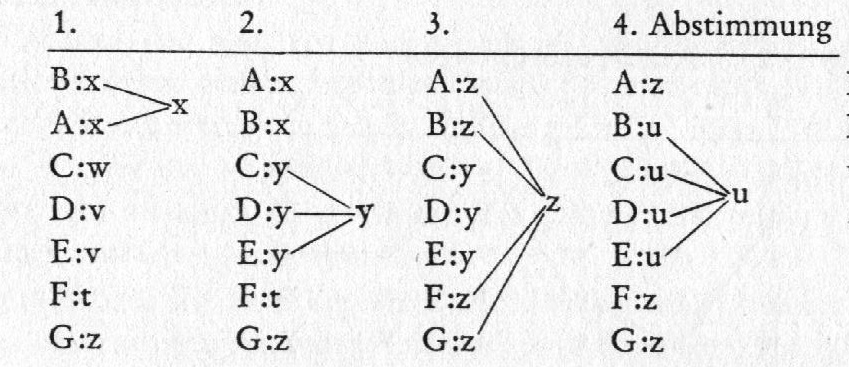
Abb.: 19.2
Mit der Koalition B, C, D, E auf der Basis u ist jedoch ein
stabiler Gleichgewichtspunkt der Koalitionsbildung erreicht, denn kein Mitglied
dieser Koalition kann mehr ein Interesse haben, irgendeine
Abstimmungsvereinbarung einzugehen auf Grundlage einer anderen Alternative:
Für
E ist die Alternative u sowieso die Spitzenalternative.
Für B, C und D wären bestimmte Alternativen zwar besser als
u, jedoch würde sich für jede dieser Alternativen höchstens ein Koalition von 3
Individuen gegenüber u zusammenbringen lassen, was für eine Gewinnkoalition nicht ausreicht.
Gleichzeitig ist die Alternative u jedoch auch die
Mehrheitsalternative, denn sie würde in paarweiser Abstimmung entsprechend den
tatsächlichen Präferenzen jede andere Alternative schlagen, wie der folgende
Ausschnitt aus der Wahlmatrix zeigt: {536}
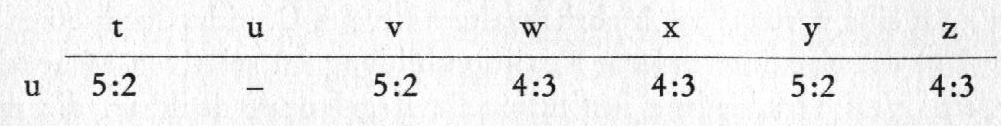
Abb. 19.3
An diesem Beispiel konnte demonstriert werden, dass auch das relative Mehrheitssystem bei eigeninteressierter Koalitionsbildung der Individuen zur Wahl der Mehrheitsalternative führt, sofern eine solche vorhanden ist. [[8] Allerdings wurde hier von starken Präferenzordnungen der Individuen ausgegangen, sodass dies Ergebnis nicht auf Situationen mit Indifferenz der Individuen gegenüber Alternativen angewandt werden kann.]
Dies Ergebnis hängt nicht mit der Wahl des obigen Beispiels zusammen, sondern kann auch folgendermaßen allgemein bewiesen werden:
Zur Vereinfachung der Ausdrucksweise soll der Ausdruck "Die Alternative x hat die Mehrheit gegenüber der Alternative y" bedeuten: "Die Anzahl der Individuen, die x gegenüber y vorziehen, ist größer als die Anzahl der Individuen, die umgekehrt y gegenüber x vorziehen". Dann ist die Mehrheitsalternative m dadurch gekennzeichnet, dass sie gegenüber jeder andern Alternative in diesem Sinne die Mehrheit hat.
Wenn nun bei einer Abstimmung nach der relativen
Mehrheitsregel irgendeine andere Alternative x die relativ meisten Stimmen
erhält und damit als kollektiv gewählt gilt, so kann nicht jedes Individuum die
für sich vorteilhafteste Koalition eingegangen sein. Denn die
Mehrheitsalternative m hat ja definitionsgemäß auch gegenüber x die Mehrheit,
sodass sich die Befürworter von m gegenüber x in ihrem eigenen Interesse {537} zu einer
für sie vorteilhaften und erfolgreichen
Koalition hätten zusammenschließen können, um die für sie vorteilhaftere
Mehrheitsalternative m durchzusetzen.
Natürlich kann eine solche rationale Koalitionsbildung in
der Realität durch die verschiedensten Faktoren behindert werden, die im
Folgenden kurz dargestellt werden sollen. (Eine eingehende Behandlung dieser
Aspekte würde den Rahmen dieser Arbeit sprengen.)
Zum einen kann
aufgrund mangelnder oder falscher Information die Interessenlage möglicher
Koalitionspartner falsch eingeschätzt werden, sodass gar kein Versuch zu einer
eigentlich möglichen Koalition gemacht wird.
Zum andern kann bei einer
terminierten Abstimmung die für Koalitionsabsprachen notwendige Zeit fehlen,
sodass auch deswegen eigentlich mögliche Abstimmungsvereinbarungen nicht zustande kommen.
Ein weiteres Hindernis für eine rationale Koalitionsbildung kann
darin liegen, dass Individuen oder Gruppen die Abstimmung als ein "Bekenntnis"
ihrer Einstellung bzw. ihrer Auffassung vom Gesamtinteresse auffassen und
deshalb ohne Rücksicht auf mögliche Gewinnchancen der entsprechenden Alternative
starr für diese abstimmen.
Ähnliche Schwierigkeiten für eine rationale
Koalitionsbildung ergeben sich dann, wenn Individuen bzw. Gruppen bestimmte
andere Individuen oder Gruppen für prinzipiell nicht koalitionsfähig halten,
selbst wenn eine solche Koalition im Einzelfall möglich und vorteilhaft wäre.
All diese Faktoren können dazu führen, dass eigentlich mögliche Gewinnkoalitionen
nicht zustande kommen und dass bei Anwendung der relativen Mehrheitsregel die
Zersplitterung der Stimmen fortbesteht, {538} sodass Alternativen mit einem sehr geringen
Prozentsatz an Stimmen die relative Mehrheit erringen können.
In diesem Fall
behinderter Koalitionsbildung wird sich auch eine vorhandene
Mehrheitsalternative u. U. nicht durchsetzen können.
Um die eigeninteressierte Koalitionsbildung im relativen
Mehrheitssystem zu fördern, sind verschiedene institutionelle Regelungen
denkbar, die die Information der Beteiligten über ihre Interessenlage fördern,
die die nötige Zeit zum Aushandeln von
Abstimmungsvereinbarungen lassen und die die Korrektur strategischer Fehler
ermöglichen.
Dies kann z. B. erreicht werden:
durch die Festlegung von Fristen
zwischen der Ankündigung einer Entscheidung und der endgültigen Beschlussfassung,
durch die Bereitstellung von Gremien für die Diskussion zwischen den Beteiligten
z. B. in Form von Ausschüssen,
durch die Ermittlung von unverbindlichen "Meinungsbildern" vor der endgültigen Abstimmung oder
durch die Vorschrift zur
wiederholten Abstimmung, wobei dann die letzte verbindlich ist. [[9] Dies entspricht der Pflicht zur mehrfachen Lesung von Gesetzesentwürfen in parlamentarischen Systemen.]
§ 115 Die Regel der absoluten Mehrheit
Um zu verhindern, dass sich Alternativen mit einem sehr
geringen Prozentsatz der Stimmen durchsetzen können und eine vorhandene
Mehrheitsalternative sich aufgrund unvollkommener Koalitionsbildung nicht
durchsetzt, kann man auch als kollektive Entscheidungs-Regel die Regel der
absoluten Mehrheit
{539} anwenden. Diese Regel besagt, dass eine
Alternative dann als kollektiv gewählt gilt, wenn sie bei einer gleichzeitigen
Abstimmung über alle Alternativen mehr als die Hälfte aller Stimmen erhält.
Häufig wird die absolute Mehrheitsregel auch so definiert, dass die erfolgreiche
Alternative nur mindestens die Hälfte aller Stimmen erhalten muss. Bei
ungerader Stimmenzahl laufen beide Varianten auf das gleiche Ergebnis hinaus.
Bei gerader Gesamtzahl der Stimmen kann die letztere Formulierung jedoch dazu
führen, dass zwei Alternativen gleichzeitig die absolute Mehrheit erreichen,
weshalb diese Formulierung hier nicht gewählt wird.
Sofern auch
Stimmenthaltungen vorkommen, kann die Regel der absoluten Mehrheit auch
dahingehend modifiziert werden, dass die siegreiche Alternative mehr als die
Hälfte der abgegebenen Stimmen erhalten muss.
Durch die Bedingung einer absoluten Mehrheit von mehr als 50% der Stimmen für die Annahme einer Alternative
wird von vornherein ein Zwang zur Bildung entsprechend großer
Abstimmungskoalitionen geschaffen. Im Unterschied zur relativen Mehrheitsregel
wirkt die absolute Mehrheitsregel damit einer Zersplitterung der Stimmen
entgegen.
Diesen Vorzug hatte bereits CONDORCET erkannt. "Er zeigt, dass die
einmalige Abstimmung zur Wahl eines Kandidaten führen kann, gegen den jeder der
übrigen Kandidaten eine Mehrheit erhalten könnte, und er zieht die
Schlussfolgerung, dass - wenn überhaupt die einmalige Abstimmung benutzt wird -
gefordert werden sollte, dass ein Kandidat mindestens die Hälfte aller
abgegebenen Stimmen erhält." [[10] BLACK 1971, S.166.] {540}
Sofern die Individuen jedoch wiederum "stur" für ihre Spitzenalternative
stimmen, so ergeben sich auch bei Anwendung der absoluten Mehrheitsregel
Probleme, da in diesem Fall häufig überhaupt keine Alternative die erforderliche
Stimmenzahl erhält. In diesem Fall bedarf es zusätzlicher Regelungen, um in
jedem Fall zu einer eindeutigen kollektiven Entscheidung zu kommen.
Eine
Möglichkeit dazu ist die Einführung einer Status-quo-Klausel, die besagt, dass
immer dann, wenn keine der Alternativen die erforderliche absolute Mehrheit der
Stimmen erhält, der Status quo als kollektiv gewählt gilt. [[11] Siehe dazu
ausführlicher unten § 135.]
Wenn die Individuen bei Abstimmungen nach der absoluten Mehrheitsregel die
für sie vorteilhaftesten Abstimmungskoalitionen eingehen, so muss sich ebenso
wie bei Abstimmungen nach der relativen Mehrheitsregel eine vorhandene
Mehrheitsalternative durchsetzen. Wenn anstatt einer vorhandenen
Mehrheitsalternative m irgendeine andere Alternative x die absolute Mehrheit
der Stimmen erhält, so kann nicht jedes Individuum die für sich vorteilhafteste
Abstimmungsvereinbarung eingegangen sein. Denn die Mehrheitsalternative m hat
ja auch gegenüber x die Mehrheit, sodass die Befürworter von m gegenüber x eine
Gewinnkoalition auf der Basis m hätten bilden können.
Die absolute Mehrheitsregel führt also genau wie die relative
Mehrheitsregel bei rationaler Koalitionsbildung aller Individuen zur Wahl einer
vorhandenen Mehrheitsalternative. Dies zeigte sich bereits am Beispiel aus Abb.
19.2, wo bei Anwendung der relativen {541} Mehrheitsregel sich die Mehrheitsalternative u
mit der absoluten Mehrheit von 4 der insgesamt 7 Stimmen durchsetzte. Dabei verhindert die
absolute Mehrheitsregel eine Koalitionsbildung ohne Erreichen des
Gleichgewichtspunktes in Form der Mehrheitsalternative, wie es bei Anwendung
der relativen Mehrheitsregel aufgrund der bereits genannten
Koalitionshindernisse geschehen kann.
Dem steht jedoch die Möglichkeit einer
Blockierung der kollektiven Entscheidung gegenüber, wenn aufgrund mangelnder
Koalitionsbildung überhaupt keine Alternative die erforderliche absolute
Mehrheit erhält.
Gewisse Schwierigkeiten ergeben sich bei Anwendung der
absoluten Mehrheitsregel, wenn Individuen zwischen Alternativen indifferent
sind und trotzdem für eine erfolgreiche Alternative die absolute Mehrheit der
Gesamtzahl aller Stimmen gefordert wird. In diesem Fall muss sich eine vorhandene
Mehrheitsalternative nicht unbedingt durchsetzen. Dies kann an einem extremen
Beispiel veranschaulicht werden.
Wenn alle Individuen bis auf eines gegenüber
allen Alternativen indifferent sind, während das eine Individuum die Alternative
m gegenüber den andern Alternativen vorzieht, so ist m die
Mehrheitsalternative, denn sie erhält im Paarvergleich mit allen andern
Individuen eine Stimme mehr.
Trotzdem muss die Mehrheitsalternative m bei einer
einmaligen Abstimmung nicht die absolute Mehrheit aller Stimmen erhalten. Wenn
sich die indifferenten Individuen der Stimme enthalten, bekommt die
Mehrheitsalternative m in diesem Fall nur eine einzige Stimme, was für die
absolute Mehrheit nicht ausreicht. Aus diesem Grunde ist es sinnvoll, für die
erfolgreiche Alternative nur die absolute Mehrheit aller abgegebenen Stimmen zu fordern,
{542} damit eine vorhandene Mehrheitsalternative sich auch
bei Indifferenz einiger Individuen durchsetzen kann.
§ 116 Das Verfahren der 'Schrittweisen Eliminierung' der Alternativen
Wenn aus irgendwelchen Gründen eine rationale
Koalitionsbildung nicht vorausgesetzt werden kann, sodass die einfachen
Verfahren nach der relativen oder absoluten Mehrheitsregel nicht sinnvoll
erscheinen, so kann man Eliminierungsverfahren anwenden, bei denen schrittweise die
jeweils schlechteste Alternative ausgeschieden wird, bis am Ende des
mehrstufigen Abstimmungsverfahrens nur noch eine einzige Alternative
übrigbleibt, die dann als kollektiv gewählt gilt. Ein derartiges
Eliminierungsverfahren, das er "erschöpfende Abstimmung" (exhaustive voting)
nennt, beschreibt BLACK. [[12] S. BLACK 1971, S.69ff.]
Dabei erhält jedes Individuum bei jedem Wahlgang eine
Stimme weniger als Alternativen zur Wahl stehen, ohne dass die Stimmen kumuliert
werden dürfen. Dadurch erhält die individuell schlechteste Alternative jeweils
von dem Individuum keine Stimme. Diejenige Alternative, die von den meisten
Individuen als die schlechteste angesehen wird und folglich am wenigsten Stimmen
erhält, scheidet dann für die folgenden Wahlgänge aus. Da bei jedem Wahlgang
eine Alternative eliminiert wird, bis am Ende nur eine Alternative übrigbleibt,
sind insgesamt soviel Wahlgänge erforderlich, wie die um 1 verminderte Anzahl
der Alternativen beträgt. {543}
Es handelt sich bei diesem Verfahren also gewissermaßen um
eine Negativ-Auswahl nach der relativen Mehrheitsregel. Man könnte stattdessen
den Individuen für jeden Wahlgang auch nur eine Stimme geben und sie auffordern,
die Stimme der für sie schlechtesten Alternative zu geben.
Zur Vereinfachung des recht umständlichen Wahlverfahrens
kann man es auf zwei Stufen beschränken, indem man bereits nach dem
ersten Wahlgang sämtliche Alternativen bis auf die zwei Alternativen mit den
meisten Stimmen eliminiert. [[13] Ein derartiges Verfahren findet z. B. bei der
französischen Präsidentenwahl Anwendung. Zu Eliminierungsverfahren s. a. DODGSON
1873 u. 1876, S.217f.] Ein solches verkürztes Eliminierungsverfahren
soll hier jedoch nicht näher untersucht werden.
Wie BLACK nachgewiesen hat, führt das
Eliminierungsverfahren der "erschöpfenden Abstimmung" im Falle eingipfliger
Präferenzen der Individuen zur Auswahl der Mehrheitsalternative. [[14] S. BLACK 1971, S.69ff.] Bei eingipfligen Präferenzen liegt für jedes Individuum die individuell schlechteste
Alternative an einem der beiden Enden der Alternativen-Skala auf der
horizontalen Achse des Koordinaten-Systems, sodass jeweils immer eine der beiden äußeren Alternativen eliminiert wird. Dies kann
an einem Beispiel mit 3 Individuen A, B und C und 4 Alternativen w, x, y und z
veranschaulicht werden: {544}
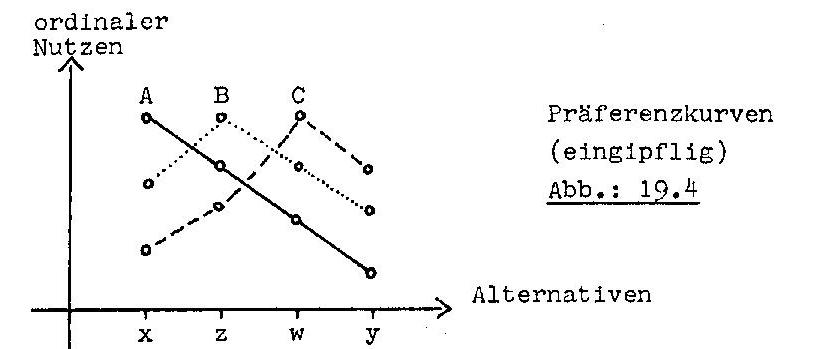
Abb. 19.4
In diesem Fall bilden x und y die äußeren Alternativen für
jedes der Individuen, sodass entweder x oder y die individuell schlechteste
Alternative ist und keine Stimme erhalten wird.
Wie anhand der Präferenzkurven
zu sehen ist, wird y von den 2 Individuen A und B keine Stimme erhalten,
während x nur von C keine Stimme erhält. Im ersten Wahlgang würde also y
eliminiert.
Im zweiten Wahlgang sind x und w die äußeren Alternativen, sodass
zwischen diesen die Entscheidung fallen muss. Hier erhält x von B und C keine
Stimme und wird damit eliminiert.
Bei der Entscheidung zwischen z und w
schließlich erhält w von A und B keine Stimme, sodass w eliminiert wird und nur
noch die Alternative z übrigbleibt und damit als kollektiv gewählt gilt.
Die
Alternative z ist aber zugleich die Mehrheitsalternative, da sie den Median der
Spitzenalternativen dieser eingipfligen Präferenzen bildet, wie oben gezeigt
wurde. Im Falle eingipfliger Präferenzen kann die Mehrheitsalternative bei
diesem Verfahren nicht eliminiert werden, da das erfordern würde, dass sie von
einer Mehrheit der Individuen als schlechter angesehen würde als eine bestimmte
andere Alternative, die am andern Rand der Alternativen-Skala steht. {545}
Wie BLACK jedoch an einem anderen Beispiel zeigt, besteht
bei fehlender Eingipfligkeit der Präferenzen die Möglichkeit, dass auch eine
vorhandene Mehrheitsalternative eliminiert wird. Bei den folgenden
Präferenzordnungen (und bei "aufrichtiger" Abstimmung, die BLACK bei seinen
Alternativen immer voraussetzt) würde die Mehrheitsalternative x bereits im
ersten Wahlgang eliminiert:
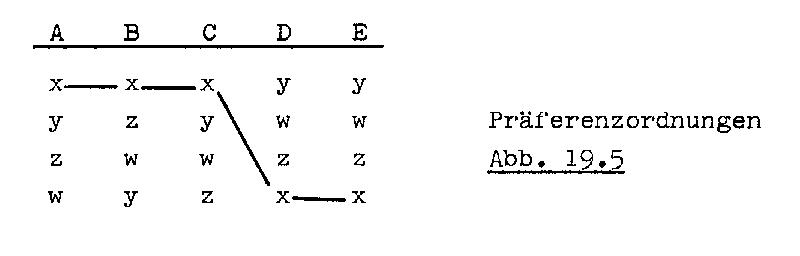
Abb.: 19.5
Im ersten Wahlgang würde die Alternative x von den
Individuen D und E als individuell schlechteste aller Alternativen keine Stimme
erhalten. Sie würde deshalb insgesamt nur 3 Stimmen bekommen, während die andern
Alternativen w, y und z je 4 Stimmen bekommen würden, da sie nur für jeweils ein
Individuum die schlechteste Alternative darstellen. Damit wäre die
Mehrheitsalternative x bereits nach dem ersten Wahlgang eliminiert. [[15] S. BLACK 1971, S.71.]
Da das
Verfahren der schrittweisen Eliminierung gewissermaßen eine Negativ-Auswahl nach
der relativen Mehrheitsregel darstellt, treten hier also ähnliche Probleme in
Bezug auf die Durchsetzung der Mehrheitsalternative bei nicht-strategischem
Abstimmungsverhalten der Individuen auf. {546}
Man könnte jedoch andererseits auch die Meinung vertreten,
dass eine Alternative wie x, die von der relativen Mehrheit der Individuen als
die schlechteste angesehen wird, schwerlich die kollektiv beste sein kann,
selbst wenn es sich um die Mehrheitsalternative handelt. Letztlich lässt sich
jedoch die Frage, welche der Alternativen im Einzelfall die kollektiv beste ist
und ein Maximum des Gesamtnutzens darstellt, nicht auf der Basis nur ordinaler
Nutzenbestimmungen beantworten, sondern erfordert eine kardinale Nutzenmessung.
[[16] Zur Beziehung zwischen der Mehrheitsalternative und der
Alternative maximalen Gesamtnutzens siehe unten § 139.]
Abgesehen von dieser Problematik und dem Aufwand der
wiederholten Wahlgänge hat das Eliminierungsverfahren jedoch den Vorteil, dass
es keine strategischen Überlegungen bei den Individuen erfordert. Die Individuen
müssen nur wissen, welches für sie die jeweils schlechteste der zur Entscheidung
stehenden Alternativen ist. Es ergibt sich dann automatisch eine gewisse
Konzentration auf kollektiv "akzeptable" Alternativen, ohne dass
Koalitionsabsprachen erforderlich sind. Das Eliminierungsverfahren erscheint
deshalb in den Fällen geeignet, wo eine rationale Koalitionsbildung aus
irgendwelchen Gründen behindert ist.
Allerdings kann es auch beim Eliminierungsverfahren zu
strategischem Abstimmungsverhalten kommen. So können hier einzelne Individuen
auch ohne jede Koalitionsbildung mit Hilfe eines "ausgeklügelten"
Abstimmungsverhaltens das Ergebnis zu ihren Gunsten {547}beeinflussen. [[17] Siehe FARQUHARSON 1969, Appendix I, wo die Ergebnisse
für "aufrichtiges" und für "ausgeklügeltes" Abstimmungsverhalten gegeben werden.]
Außerdem ist natürlich auch im Rahmen des Eliminierungsverfahrens Koalitionsbildung möglich, wodurch die Ergebnisse
völlig verändert werden können. Im Beispiel aus Abb. 19.5 könnten z. B. A, B und
C durch eine gemeinsame Abstimmungsstrategie die für sie vorteilhafteste
Mehrheitsalternative x durchsetzen, indem sie im 1. Wahlgang geschlossen gegen
w stimmen, im 2. Wahlgang geschlossen gegen z und im 3. Wahlgang gegen y.
Auch für das Eliminierungsverfahren gilt also, dass bei
rationaler Koalitionsbildung aller Individuen eine vorhandene
Mehrheitsalternative m sich durchsetzt, sofern keine Indifferenzen vorkommen.
Wenn sich statt m irgendeine andere Alternative x durchsetzt, so müssen einige
Individuen von ihrer Interessenlage her gesehen strategische Fehler gemacht
haben. Diejenige Mehrheit der Individuen, die m gegenüber x vorzieht, hätte zur
Durchsetzung von m nur vereinbaren müssen, dass sie bei jedem der Wahlgänge
jeweils geschlossen eine der übrigen Alternativen nicht wählt, sodass diese
Alternative eliminiert wird. Damit würde die Mehrheitsalternative m schließlich
übrig bleiben.
§ 117 Die Rangplatz-Methode der Abstimmung
Während die bisherigen Abstimmungsverfahren nur eine
ordinale Erfassung der individuellen Nutzen beinhalten, {548} versuchen manche Verfahren auch, die individuellen
Nutzendifferenzen zwischen den Alternativen zu berücksichtigen.
Eines dieser
Verfahren ist die Rangplatz-Methode, bei der die Rangplätze der Alternativen kardinal interpretiert werden, indem der Abstand von einem Rangplatz zum
nächsten bei jedem Individuum immer als eine Nutzeneinheit gewertet wird. [[18]
MUSGRAVE nennt dies Verfahren 'plurality rule'. S.
MUSGRAVE 1959, S.129.]
Entsprechend der Zahl der Rangplätze, die eine Alternative höher eingestuft ist
als eine andere, bekommt sie damit auch einen höheren Nutzenwert. Man kann z. B.
der schlechtesten Alternative jedes Individuums den Punktwert "0" zuordnen, der
zweitschlechtesten den Punktwert "1", der drittschlechtesten den Punktwert "2"
usw. bis hinauf zu den Spitzenalternativen. Dann werden die Punktwerte der
verschiedenen Alternativen addiert und diejenige Alternative, die den höchsten
Gesamtwert erreicht, gilt als kollektiv gewählt.
Ein derartiges Verfahren wurde
bereits 1781 von BORDA vorgeschlagen, weshalb es auch als BORDA-Kriterium
bezeichnet wird. [[19] Siehe BLACK 1971, S.156f. u. 59ff.] ARROW bezeichnet diese Methode als "Rangordnungs-Methode der
Abstimmung" (rank-order method of voting). [[20] S. ARROW 1963, S.27.]
Diese Methode wurde von DODGSON als
das beste aller möglichen Wahlverfahren angesehen, wobei allerdings zu
berücksichtigen ist, dass er Abstimmungsstrategien als unzulässig ansah und nicht
erkannte, dass gerade die Anwendung kollektiver Abstimmungsstrategien zur
Durchsetzung der Mehrheitsalternative führt. [[21] S. DODGSON 1873, S.221.]
{549}
Bei der Rangplatz-Methode siegt bei aufrichtigen
Präferenzäußerungen diejenige Alternative, die bei allen Individuen den höchsten
durchschnittlichen Rangplatz einnimmt. Dies kann an den
folgenden Präferenzordnungen von 5 Individuen A bis E und 5 Alternativen v bis z veranschaulicht werden. Dabei sind
die Punktwerte in Klammern hinter die Alternativen gesetzt:
Präferenzordnungen (mit Punktwerten)
| A | B | C | D | E |
| z(4) | y(4) | z(4) | y(4) | w(4) |
| y(3) | v(3) | y(3) | x(3) | z(3) |
| x(2) | w(2) | w(2) | v(2) | y(2) |
| w(1) | x(1) | v(1) | z(1) | x(1) |
Abb.: 19.6
Die Punktsummen für die einzelnen Alternativen sind: v = 6;
w = 9; x = 7; y = 16 und z = 12. In diesem Beispiel erreicht die Alternative y
mit 16 Punkten den höchsten Gesamtwert. Ihr durchschnittlicher Punktwert pro
Individuum ist 16:5 = 3,2. Dies entspricht einem durchschnittlichen Rangplatz
von 5 - 3,2 = 1,8.
Die Rangplatz-Methode kann man auch dahingehend
interpretieren, dass sie die Alternativen nach der Gesamtzahl der positiven
Stimmen ordnet, die jede Alternative bei allen Paarvergleichen zusammen erhalten
würde, wenn alle Individuen aufrichtig abstimmen. [[22] Siehe dazu ausführlich BLACK 1971, S.59ff.]
{550}
Dies kann anhand der Wahlmatrix zu den Präferenzordnungen
aus Abb. 19.6 verdeutlicht werden:
Wahlmatrix zu Abb. 19.6 mit Gesamt-Stimmenzahl
| v | w | x | y | z | gesamt | |
| v | - | 2:3 | 2:3 | 0:5 | 2:3 | 6:14 |
| w | 3:2 | - | 3:2 | 1:4 | 2:3 | 9:11 |
| x | 3:2 | 2:3 | - | 0:5 | 2:3 | 7:13 |
| y | 5:0 | 4:1 | 5:0 | - | 2:3 | 16:4 |
| z | 3:2 | 3:2 | 3:2 | 3:2 | - | 12:8 |
Abb.: 19.7
Wie man sieht, werden die Alternativen durch die Gesamtzahl
der Stimmen für die Alternativen genauso geordnet wie durch die
Rangplatz-Methode der Abstimmung, denn die Gesamtstimmenzahl entspricht genau
dem Gesamtpunktewert.
Die Annahmen, die bei einer derartigen kardinalen
Interpretation von Präferenzrangordnungen gemacht werden müssen, sind bereits
von BORDA genannt worden. Zum einen muss vorausgesetzt werden, dass die
Nutzendifferenz von einem Rangplatz zum nächsten bei ein und demselben
Individuum immer gleich ist. Zum andern muss die Nutzendifferenz zwischen der
besten und der schlechtesten Alternative für alle Individuen gleich groß sein.
BORDA interpretiert die Rangordnung, die ein Individuum drei Kandidaten A, B und
C entsprechend der alphabetischen Reihenfolge gegeben hat, folgendermaßen: "Ich
sage, dass der Grad der Überlegenheit, den dieser Wähler A über B gegeben hat,
als der gleiche Grad von Überlegenheit angesehen werden sollte wie der, den er B
gegenüber C zugeordnet hat. ... Ich behaupte weiter, dass - wegen der angenommenen
{551} Gleichheit zwischen allen Wählern - jeder Rangplatz, der
durch einen Wähler vergeben wird, als gleichwertig angesehen werden muss ." [[23]
S. BORDA nach BLACK 1971,
S.157.]
Beide Annahmen sind jedoch problematisch. Wenn z. B. die
Nutzendifferenzen zwischen allen aufeinanderfolgenden Alternativen gleich sein
sollen, so könnte allein durch Ausscheiden oder Hinzukommen von Alternativen die
Nutzendifferenz zwischen zwei Alternativen verändert werden, obwohl beide
Alternativen völlig unverändert geblieben sind. ARROW verdeutlicht diese
Problematik der Rangplatz-Methode an folgendem Beispiel mit 3 Wählern und 4
Kandidaten:
Präferenzordnungen (mit Punktwerten)
| A | B | C |
| x(3) | x(3) | z(3) |
| y(2) | y(2) | w(2) |
| z(1) | z(1) | x(1) |
| w(0) | w(0) | y(0) |
Abb.: 19.8
Die Punktergebnisse der Alternativen sind: w = 2; x = 7; y
= 4 und z = 5. "Bei dem angegebenen Wahlsystem wird x gewählt. Wenn y als
Kandidat ausscheidet, so sollte sicherlich das Verfahren - angewandt auf die
verbleibenden Kandidaten - dasselbe Resultat ergeben, vor allem da in diesem
Fall y gemäß der Einstellung jedes Individuums schlechter ist als x; aber wenn y
ausscheidet, würde das angegebene Wahlsystem Punktgleichheit zwischen x und z
ergeben." [[24] ARROW 1963, S.27. Für ARROW ist die Rangplatz-Methode ein
Beispiel für eine kollektive Entscheidungs-Regel, die die Bedingung der "Unabhängigkeit von irrelevanten Alternativen" verletzt. S. dazu oben § 37/3.
Die Problematik dieses Verfahrens liegt jedoch in der schematisierten Nutzen"messung".] Dies zeigt die folgende Tabelle: {552}
Präferenzordnungen (mit Punktwerten)
|
A |
B |
C |
|
x(2) |
x(2) |
z(2) |
|
z(1) |
z(1) |
w(1) |
|
w(0) |
w(0) |
x(0) |
Abb.: 19.9
Die Punktergebnisse der Alternativen sind nach Ausscheiden
der Alternative y jetzt: w = 1; x = 4 und z = 4.
Diese Problematik der Rangplatz-Methode sieht auch BLACK,
wenn er schreibt: "Ein Wähler misst die relativen Verdienste (merits) der
Kandidaten nicht in Form von Punkten. ... Und wenn dies so ist, dann ist auf
diesem Wege keine Rechtfertigung des BORDA-Kriteriums möglich." [[25] BLACK 1971, S.65.]
Auch die in
der Rangplatz-Methode implizierte interpersonale Angleichung der
Nutzenspannweite zwischen der individuell besten und der schlechtesten
Alternative erscheint unbegründet, denn es kann ja ohne weiteres sein, dass für
ein Individuum alle Alternativen nahezu gleichwertig sind, während für ein
anderes Individuum gravierende Unterschiede bestehen. [[26] Zur Normalisierung subjektiver Nutzen s.o. § 41.]
Ein entscheidendes Problem für die praktische Anwendbarkeit
der Rangplatz-Methode ist jedoch seine Anfälligkeit für strategisches Vorgehen
der Individuen. Wenn z. B. ein Individuum eine Spitzenalternative hat, die jedoch
keine Erfolgsaussichten besitzt, so ist es für das Individuum vorteilhafter, die
hohe Punktzahl des ersten Rangplatzes lieber einer aussichtsreicheren
Alternative zukommen zu lassen.{553}
Dies kann am Beispiel aus Abb. 19.6 veranschaulicht werden.
Wenn den drei Individuen A, C und E klar wird, dass bei "aufrichtiger"
Aufstellung ihrer individuellen Präferenzordnungen die Alternative y siegen
würde, so könnten sie der Alternative z zum Sieg verhelfen, die von ihnen
gegenüber y vorgezogen wird. Sie müssen dazu nur geschlossen die Alternative z
auf den ersten Rangplatz setzen. Dadurch würde die Alternative z allein von
dieser Dreier-Koalition 12 Punkte erhalten. Wenn sie nun gleichzeitig die
Alternative y auf den letzten Platz setzen, so kann diese höchstens noch
zusammen 8 Punkte von den beiden andern Individuen erhalten, sodass z erfolgreich
ist.
Wie man aus der Wahlmatrix in Abb. 19.7 ersieht, ist z in diesem Beispiel
die Mehrheitsalternative, denn sie ist im Paarvergleich jeder anderen
Alternative überlegen. Obwohl also nach der Rangplatz-Methode eigentlich die
Alternative y siegen müsste, da diese den höchsten durchschnittlichen Rangplatz
in den individuellen Präferenzordnungen einnimmt, kommt es auch in diesem Fall
zu einer Durchsetzung der Mehrheitsalternative aufgrund rationaler
Koalitionsbildung.
Dass dies generell so sein muss, kann durch folgende
Überlegung bewiesen werden. Wenn nämlich anstelle der Mehrheitsalternative m
irgendeine andere Alternative x siegt, so haben einige Individuen nicht die für
sie vorteilhafteste Abstimmungsvereinbarung abgeschlossen. Da die Befürworter
von m gegenüber x in der Überzahl sein müssen, können sie immer die von ihnen
vorgezogene Mehrheitsalternative m durchsetzen, indem sie geschlossen m an die
erste und x an die letzte Stelle setzen. Sofern mit solchen
Abstimmungsstrategien zu rechnen ist - und man kann {554} sie praktisch nicht verhindern - , ergibt die
Rangplatz-Methode im Endeffekt also keine bessere Berücksichtigung der
Präferenzintensitäten als das viel einfachere relative Mehrheitssystem. [[27]
Eine zusätzliche Komplikation der Rangplatz-Methode
ergibt sich noch aus der Möglichkeit zum Zurückziehen von Alternativen aus
strategischen Erwägungen.]
§ 118 Die Punkte-Methode der Abstimmung
Ein anderes Verfahren, bei dem die Individuen im Prinzip
ihre Präferenzintensitäten bzw. ihre Nutzendifferenzen ausdrücken können, ist
die Punkte-Methode. "Bei dieser Methode wird eine bestimmte Anzahl von Punkten
festgelegt, die jeder Wähler zu seiner Verfügung haben soll; er kann sie alle
einem Kandidaten zuordnen oder sie zwischen mehreren Kandidaten aufteilen im
Verhältnis zu ihrer Vorzugswürdigkeit (eligibility); und der Kandidat ist der
Gewinner, der die größte Gesamtzahl an Punkten erhält. [[28] DODGSON 1973, S.218. Er nennt die Punkte-Methode "method
of marks". MUSGRAVE nennt sie "point voting". S. MUSGRAVE 1959, S.130.]
Bei diesem Verfahren wird durch die Normalisierung der für
jedes Individuum verfügbaren Punktemenge vorausgesetzt, dass die Nutzensumme
aller Alternativen für jedes Individuum gleich ist. Im Unterschied zur
Rangplatz-Methode sind jedoch bei der Punkte-Methode die Nutzendifferenzen
zwischen den Alternativen nicht festgelegt, sodass hier in Bezug auf die
Beschaffenheit der individuellen Nutzenfunktionen weniger extreme Annahmen
gemacht werden. {555}
Die Punkte-Methode kann an einem Beispiel verdeutlicht
werden, bei dem die 3 Individuen A, B und C die 3 Alternativen x, y und z durch
die Aufteilung von 10 Punkten bewerten sollen:
Präferenzordnungen (mit Punktwerten)
| A | B | C |
| x(9) | y(5) | z(7) |
| y(1) | z(3) | y(2) |
| z(0) | x(2) | x(1) |
Abb.: 19.10
Das Ergebnis der Punkte-Methode wäre hier x = 12, y = 8 und
z = 10 Punkte, sodass die Alternative x als kollektiv gewählt gilt.
Im Prinzip hätte ein solches Verfahren gegenüber bloßen
Präferenzrangordnungen der Alternativen erhebliche Vorteile, da hier auch
Nutzendifferenzen beliebig genau ausgedrückt werden können. So schreibt auch
DODGSON: "Diese Methode würde .. absolut perfekt sein, wenn nur jeder Wähler
alles in seiner Macht stehende tun wollte, um die Wahl desjenigen Kandidaten
sicherzustellen, der allgemein der akzeptabelste sein sollte; in diesem Fall
würde er bemüht sein, dass seine Punkte genau seine Einschätzung der relativen
Vorzugswürdigkeit aller Kandidaten wiedergeben, sogar bei denen, die er am
wenigsten gewählt sehen möchte." [[29] DODGSON 1873, S.218. DODGSON diskutiert die
Wahlverfahren anhand der Stellenbesetzungen in Universitätsgremien, wo es auf
die Qualifikation der Kandidaten ankommt.]
Allerdings lädt die Punkte-Methode zur Anwendung
vorteilhafter Abstimmungsstrategien geradezu ein. Selbst wo
Abstimmungsvereinbarungen ausgeschlossen werden, {556} können die Individuen "ausgeklügelte" individuelle
Strategien verwenden. Dies hat auch schon DODGSON erkannt: "Aber wir sind nicht
genügend selbstlos und mit Gemeinsinn ausgestattet, um irgendeine Hoffnung auf
das Erreichen eines derartigen Ergebnisses zu setzen. Jeder Wähler würde merken,
dass es für jeden andern Wähler möglich ist, die gesamte Punktemenge seinem
favorisierten Kandidaten zu geben und allen übrigen Kandidaten null Punkte zu
geben; und er würde den Schluss ziehen, dass er für den von ihm selber
favorisierten Kandidaten dasselbe tun muss." [[3O] DODGSON 1873, S.218.] DODGSON zieht daraus den Schluss,
dass die Punkte-Methode in dem zu erwartenden Fall, dass alle Wähler ihrem
Favoriten die gesamte Punktmenge geben, auf das gleiche hinausläuft wie die
relative Mehrheitsregel, nur dass die Wähler den Kandidaten jetzt statt einer
Stimme z. B. 10 Punkte geben. [[31] Zu ähnlichen Ergebnissen kommt auch MACKSCHEIDT 1973 in
Bezug auf die Punkte-Methode.]
Sofern jedoch alle Individuen die für sie vorteilhaftesten
Abstimmungsvereinbarungen eingehen, so setzt sich auch bei der Punkte-Methode
eine vorhandene Mehrheitsalternative durch. Dies kann am Beispiel aus Abb. 19.10 veranschaulicht werden, wo die Alternative y die Mehrheitsalternative
ist. Bei aufrichtiger Wiedergabe der individuellen Nutzendifferenzen wäre hier
die Alternative x gewählt worden. Die Individuen B und C könnten jedoch die Wahl
der für sie besseren Alternative y durchsetzen, indem sie ihre gesamten 10
Punkte geschlossen y zuteilen. {557}
Wenn alle Individuen die für sie vorteilhaftesten
Abstimmungsvereinbarungen eingehen, so muss sich auch bei der Punkte-Methode eine
Gewinnkoalition auf der Basis einer vorhandenen Mehrheitsalternative bilden,
sodass man auch in diesem Fall besser gleich das einfachere und "ehrlichere"
Verfahren nach der einfachen Mehrheitsregel anwendet.
§ 119 Das Verfahren der 'paarweisen Abstimmung'
Als letztes Abstimmungsverfahren soll das Verfahren der
'paarweisen Abstimmung' analysiert werden, das bereits vorne als CONDORCET-Kriterium beschrieben wurde. Wenn die Individuen hierbei immer "aufrichtig" abstimmen, so bekommt eine vorhandene Mehrheitsalternative in
allen Abstimmungen die Mehrheit und ist damit kollektiv gewählt.
Wenn einige
Individuen jedoch "ausgeklügelte" individuelle Abstimmungsstrategien oder gar
kollektive Abstimmungsvereinbarungen anwenden, so können sie einer vorhandenen
Mehrheitsalternative u. U. eine Niederlage in einer der paarweisen Abstimmungen
beibringen und damit verhindern, dass diese als kollektiv gewählt gilt.
Dies kann
am Beispiel der folgenden Präferenzordnungen für 3 Individuen A, B und C und 3
Alternativen x, y und z veranschaulicht werden:
Präferenzordnungen
| A | B | C |
| x | y | z |
| y | z | y |
| z | x | x |
Abb.: 19.11
In diesem Beispiel ist y die Mehrheitsalternative, denn sie wird sowohl gegenüber x als auch gegenüber z von 2 der 3 Individuen vorgezogen, wie die folgende {558} Wahlmatrix zeigt:
Wahlmatrix zu
Abb.19.11
|
|
x |
y |
z |
|
x |
- |
1:2 |
1:2 |
|
y |
2:1 |
- |
2:1 |
|
z |
2:1 |
1:2 |
- |
Abb.: 19.12
Individuum C könnte jedoch in diesem Fall bei Anwendung des
Verfahrens der paarweisen Abstimmung die Wahl von y dadurch verhindern, dass es
bei der Abstimmung zwischen y und x nicht für y stimmt, was seiner eigentlichen
Präferenz entsprechen würde, sondern für x. Dadurch würde y gegenüber x
unterliegen und wäre damit gescheitert.
Diese Problematik beim Verfahren der paarweisen Abstimmung
war bereits von DODGSON betont worden. [[32] Siehe DODGSON 1876, S.232ff.] Wenn ein Teil der Individuen
strategisch abstimmt, so können sie verhindern, dass eine vorhandene
Mehrheitsalternative in sämtlichen paarweisen Abstimmungen erfolgreich bleibt,
es sei denn, die Mehrheitsalternative ist zugleich die Spitzenalternative für
eine absolute Mehrheit der Individuen.
DODGSON gibt auch das Rezept für eine
derart "destruktive" Abstimmungsstrategie an: "Bei jeder Entscheidung zwischen
zwei Ergebnissen (issues), wo du keines von beiden willst, stimme gegen das
beliebteste. Es mag dann irgendein Ergebnis geben, das bei paarweiser Abstimmung
jedes andere geschlagen hätte, sofern alle gemäß ihrer wirklichen Meinung
gestimmt hätten: aber durch die Befolgung dieser Regel kann es dir gelingen, {559] es ein einziges Mal zu schlagen durch Herbeiführen
einer zyklischen Mehrheit. Und das mag dem Ergebnis, das du wünschst, eine
Chance geben, die es sonst nicht gehabt hätte." [[33] DODGSON 1876, S.233.]
Allerdings kann durch eine
derartige Abstimmungsstrategie immer nur eine eigentlich vorhandene
Mehrheitsalternative zu Fall gebracht werden, es kann jedoch nicht positiv eine
andere Alternative durchgesetzt werden.
Wie DODGSON feststellt, ist es praktisch unmöglich zu
verhindern, dass derart "unaufrichtig" abgestimmt wird. Er schlägt zur Eindämmung
solchen Verhaltens vor, dass einleitend eine Abstimmung nach der absoluten
Mehrheitsregel durchgeführt wird, die allerdings geheim vollzogen werden soll,
um strategischem Abstimmungsverhalten die Informationsgrundlage zu entziehen.
Durch diese Abstimmung kann dann festgestellt werden, welches Individuum bei den
folgenden paarweisen Abstimmungen geänderte Präferenzen zeigt. Bekommt jedoch
eine Alternative auf Anhieb die absolute Mehrheit, so sind die folgenden paarweisen Abstimmungen überflüssig.
[[34] Siehe DODGSON 1876, S.233.]
Wenn jedoch nicht nur einige sondern alle Individuen die
für sie vorteilhaftesten Abstimmungsvereinbarungen eingehen, so setzt sich auch
beim Verfahren der paarweisen Abstimmung eine vorhandene Mehrheitsalternative m
durch.
Dies kann wiederum in negativer Beweisführung gezeigt werden. Wenn statt
m nämlich irgendeine andere Alternative x sich durchsetzt, so müssen einige
Individuen strategische Fehler gemacht haben. {560} In diesem Fall hätten diejenigen Individuen, für die m
besser ist als x, nur vereinbaren müssen, bei allen paarweisen Abstimmungen für
m zu stimmen, um mit ihrer Mehrheit die für sie bessere Alternative m anstelle
von x durchzusetzen. Bei rationaler Koalitionsbildung aller Individuen setzt
sich also auch beim Verfahren der paarweisen Abstimmung eine vorhandene
Mehrheitsalternative durch.
Allerdings ist das Verfahren aufgrund der Vielzahl
der Paarvergleiche recht umständlich, und wenn sich bei strategischem
Abstimmungsverhalten der Individuen mit der Mehrheitsalternative kein anderes
Ergebnis einstellt als bei Anwendung der relativen Mehrheitsregel, so wird man
gleich dies verhältnismäßig einfach durchzuführende Verfahren wählen.
§ 120 Ein Äquivalenz-Theorem für alle gleichgewichtigen Abstimmungsverfahren
In den vorangegangenen Paragraphen wurde für verschiedenste
Abstimmungsverfahren festgestellt, dass sie bei rationaler Koalitionsbildung der
Individuen zur Auswahl einer vorhandenen Mehrheitsalternative führen, also in
Bezug auf das Ergebnis äquivalent sind. Im Folgenden sollen diese Ergebnisse zu
einem Theorem verallgemeinert werden. Dieses Äquivalenz-Theorem
kann man folgendermaßen formulieren: "Alle Wahlverfahren, bei denen die Individuen einen
gleichgewichtigen Einfluss auf die kollektive Entscheidung haben, führen zur
Auswahl einer vorhandenen Mehrheitsalternative, wenn alle Individuen die für
sie vorteilhaftesten Abstimmungsvereinbarungen eingehen." {561}
Bevor dies Theorem bewiesen wird, ist vorweg noch zu
klären, was unter einem "gleichgewichtigen Einfluss" der Individuen zu
verstehen ist.
Ein individuell gleichgewichtiges Wahlverfahren soll durch
folgende Eigenschaften gekennzeichnet sein:
1. Sofern das Verfahren mehrere Abstimmungen erfordert,
sind alle Individuen an allen Abstimmungen beteiligt.
2. Bei jeder einzelnen Abstimmung hat jedes Individuum die gleiche Stimmen- bzw.
Punktezahl zu vergeben.
Diese Bedingungen, die jedem Individuum einen gleich großen
Einfluss auf die kollektive Entscheidung sichern, werden von allen besprochenen
Wahlverfahren erfüllt. Sie werden jedoch z. B. nicht von Veto-Regeln erfüllt, die
ja eine Status-quo-Klausel enthalten. Denn für die Durchsetzung des Status quo
sind dann ja weniger Stimmen erforderlich als für die Durchsetzung der übrigen
Alternativen. So ist z. B. bei der Regel der Zwei-Drittel-Mehrheit mit
Status-quo-Klausel - die übrigens besser Ein-Drittel-Veto-Regel hieße - für die
Durchsetzung des Status quo nur ein Drittel aller Stimmen erforderlich, während
für die Durchsetzung aller übrigen Alternativen mehr als zwei Drittel der
Stimmen erforderlich sind. Wenn ein Drittel der Individuen durch ihr Veto den
Status quo durchsetzt, so haben diese einen gewichtigeren Einfluss auf die
kollektive Entscheidung als die übrigen zwei Drittel. Damit hat aber ein
Individuum, das Mitglied der Sperrminorität ist, ein größeres Gewicht als eines
der übrigen Individuen, sodass das Verfahren nicht als individuell
gleichgewichtig angesehen werden kann.
{562}
Der Beweis des Äquivalenztheorems für gleichgewichtige
Wahlverfahren kann wiederum am einfachsten negativ geführt werden, indem
nachgewiesen wird, dass, wenn anstatt einer vorhandenen Mehrheitsalternative m
irgendeine andere Alternative x erfolgreich ist, zumindest einige Individuen
nicht die für sie vorteilhafteste Abstimmungsvereinbarung eingegangen sind.
Die
Anzahl der Individuen, die m gegenüber x vorziehen, ist ja größer als die Anzahl
der Individuen, die umgekehrt x gegenüber m vorziehen, denn m hat als
Mehrheitsalternative gegenüber jeder andern Alternative die Mehrheit.
Wenn aber
jedes Individuum auf die kollektive Entscheidung einen gleichgewichtigen Einfluss
hat, so haben die Befürworter von m gegenüber x geschlossen immer einen größeren
Einfluss auf die kollektive Entscheidung als die Befürworter von x, denn sie
sind zahlenmäßig überlegen. Sie können also eine gemeinsame
Strategie vereinbaren, um an Stelle von x die von ihnen vorgezogene
Mehrheitsalternative m durchzusetzen. [[35] Dies Äquivalenz-Theorem macht den engen Zusammenhang
zwischen dem Mehrheitsprinzip und der Bedingung des gleichen Einflusses für
jedes Individuum deutlich. S. dazu unten § 131. Übrigens wäre es sinnvoll, den
Beweis auch noch in formalisierter Form zu geben.]
Mit diesem Nachweis, dass die verschiedensten Wahlverfahren
zum gleichen Ergebnis in Form einer vorhandenen Mehrheitsalternative gelangen,
sofern den Individuen dabei nur gleiches Gewicht zukommt und eine rationale
Koalitionsbildung stattfindet, vereinfacht sich die Suche nach geeigneten
Wahlverfahren erheblich. Angesichts dieser Sachlage ist es auch verständlich,
warum in der Praxis fast nur das relative und das absolute Mehrheitssystem
Anwendung finden. {563} Diese Verfahren erfordern nur eine einzige Abstimmung
und
sind auf die Abgabe einer Stimme beschränkt, sodass sie durch Handaufheben
vollzogen werden können.
Weiterhin unterstreicht das Äquivalenz-Theorem noch einmal
die besondere Bedeutung der Mehrheitsalternative, wie sie in § 110 definiert
wurde. Diese Mehrheitsalternative ist gewissermaßen das unsichtbare
Gravitationszentrum für die kollektiven Entscheidungen aller individuell
gleichgewichtigen Abstimmungsverfahren. Es handelt sich dabei also nicht um
irgendein willkürlich gewähltes Entscheidungskriterium bzw. um irgendeine
Spielart des Mehrheitsprinzips unter andern.
Zum andern ist es wichtig festzuhalten, dass die
Durchsetzung der Mehrheitsalternative in den verschiedenen Abstimmungsverfahren
(abgesehen von der paarweisen Abstimmung) gerade dadurch zustande kommt, dass die
Individuen nicht "aufrichtig" für ihre jeweilige Spitzenalternative stimmen,
sondern so abstimmen, dass das Ergebnis für sie den größten Nutzen
erbringt. Derartig "unaufrichtiges" Abstimmungsverhalten stellt also hier kein
auszumerzendes Problem dar, sondern im Gegenteil: die Anwendung
eigeninteressierter Abstimmungsstrategien und die Bildung entsprechender
Koalitionen sollte gerade gefördert werden, wenn man der Mehrheitsalternative
zur Durchsetzung verhelfen will. [[36] Zur normativen Beurteilung der Mehrheitsalternative s. u. § 139.] {564}
Man kann hier also im Gegensatz zur Meinung von BLACK und
anderen auf eine Abstimmungsmoral zugunsten "aufrichtiger"
Präferenzäußerungen verzichten, da gerade das eigeninteressierte Abstimmungsverhalten
der Individuen quasi automatisch zur Durchsetzung der Mehrheitsalternative
führt, sofern eine solche vorhanden ist und die Bedingungen rationaler
Koalitionsbildung gegeben sind. Hier wirkt also eine "unsichtbare Hand" ähnlich
wie im Eigentum-Vertrags-System unter Konkurrenzbedingungen, wo allein durch das
eigeninteressierte Verhalten der Individuen ein pareto-optimaler Zustand
hergestellt wird und deshalb auf eine moralische Normierung des individuellen
Verhaltens verzichtet werden kann. [[37] Zur Pareto-Optimalität des Konkurrenzgleichgewichts und
seiner normativen Kritik s. o. die §§ 103 u. 104.]
Insofern ist es eigentlich unangebracht, von einem "unaufrichtigen" Abstimmungsverhalten zu sprechen, wenn ein Individuum nicht für
seine aussichtslose Spitzenalternative stimmt. Stattdessen sollte man hier von
einem "eigeninteressierten" oder "rationalen" und "strategischen" Verhalten
sprechen, denn ein solches Verhalten ist ja im Interesse einer Durchsetzung der
Mehrheitsalternative nur erwünscht. Es müssen dazu bei Mehrheitsabstimmungen
möglichst alle Hindernisse der Information und Kommunikation zwischen den
Beteiligten beseitigt werden, die einer solchen rationalen Koalitionsbildung im
Wege stehen könnten. Nur wenn diese Hindernisse nicht beseitigt werden können,
ist zur Bestimmung der Mehrheitsalternative eine direkte Erfassung der
tatsächlichen individuellen Präferenzen notwendig. {565}
[[ Der folgende Teil dieses Paragraphen
wurde 1979 hinzugefügt. Siehe zum Folgenden auch § 135.
Abschließend muss noch eine Komplikation im Zusammenhang mit dem
Äquivalenztheorem erörtert werden, die durch die Möglichkeit eines
unentschiedenen Ausgangs des Abstimmungsverfahrens bei Stimmengleichheit
entsteht.
Der Beweis des Aquivalenztheorems wurde negativ geführt: Es wurde gezeigt, dass
sich bei rationaler Koalitionsbildung und individuell gleichgewichtigem
Abstimmungsverfahren keine andere Alternative anstelle einer vorhandenen
Mehrheitsalternative durchsetzen kann. Der Schluss, dass sich dann die
Mehrheitsalternative durchsetzen muss, ist jedoch nur dann zwingend, wenn sich
überhaupt eine der Alternativen durchsetzen muss. Solange jedoch die Möglichkeit
eines "Patts" mit unentschiedenem Ausgang existiert, ist die Durchsetzung einer
vorhandenen Mehrheitsalternative nicht gewährleistet.
Dies kann anhand des folgenden Beispiels demonstriert werden, bei dem 4
Individuen nach der relativen Mehrheitsregel abstimmen:
Präferenzordnungen
| A | B | C | D |
| y | z | x | y |
| z | y | y | x |
| x | x | z | z |
Abb.:19.13
Bei dieser
Interessenkonstellation ist y die Mehrheitsalternative, da y im Paarvergleich
sowohl x als auch z mit 3:1 überlegen ist.
In diesem Fall kann jedoch Individuum B die Durchsetzung der
Mehrheitsalternative y verhindern und ein Patt herbeiführen, indem es für x
stimmt, obwohl x seine schlechteste Alternative ist. Dann erhalten x und y bei
einer Abstimmung nach der relativen Mehrheitsregel je 2 Stimmen, so dass der
Ausgang der Abstimmung wegen Stimmengleichheit unentschieden ist. Ähnliche
Möglichkeiten zur Verhinderung einer Mehrheitsalternative durch bewusstes
Herbeiführen eines Patt existieren auch in andern Abstimmungsverfahren.
Damit stellt sich die Frage, ob es Möglichkeiten zur Verhinderung solcher
"obstruktiven" Abstimmungsstrategien gibt.
Die Problematik entsteht vor allem deshalb, weil es die Möglichkeit eines
unentschiedenen Ausgangs gibt. Wenn man das Resultat der Abstimmung nicht kennt,
kann man es auch nicht bewerten und damit verschwindet die Möglichkeit einer
rationalen Entscheidung. Unter den Bedingungen eines unentschiedenen Ausgangs
kann man auch nichts darüber aussagen, ob die bewusste Herbeiführung eines Patt
im obigen Beispiel für B nun vorteilhaft war oder nicht.
Eine gebräuchliche Methode, um in jedem Fall ein Resultat sicherzustellen, ist
die Einfügung eines Status-quo-Klausel, die besagt, dass im Falle eines Patts
der Status quo als kollektiv gewählt gilt. Ein rationales Individuum wird unter
dieser Bedingung nur dann bewusst ein Patt herbeiführen, wenn der Status quo für
es besser ist als diejenige Alternative, die sonst gewinnen würde.
Zu fragen ist, ob durch die Einfügung einer solchen Status-quo-Klausel die
Durchsetzung einer vorhandenen Mehrheitsalternative in jedem Fall sichergestellt
werden kann.
Um bei Existenz einer Status-quo-Klausel das rationale Verhalten der Individuen
bestimmen zu können, ist es erforderlich, jeweils den Status quo als
Alternative in die Präferenzordnungen mit einzubeziehen. Die folgende fiktive
Tabelle ergänzt die obige Tabelle Abb.: 19.13 um die individuellen Präferenzen
in Bezug auf den Status quo (sq):
Präferenzordnungen
| A | B | C | D |
| y | z | x | y |
| z | (sq) | y | (sq) |
| x | y | (sq) | x |
| (sq) | x | z | z |
Abb.: 19.14
In diesem Beispiel ist es
für B vorteilhaft, durch Stimmabgabe für x bewusst ein Patt zwischen x und y
herbeizuführen, denn der dann sich ergebende Status quo wird von B gegenüber der
Mehrheitsalternative y vorgezogen.
Trotzdem führt das obstruktive Abstimmungsverhalten von B bei Rationalverhalten
auch der anderen Individuen hier nicht zum Patt. Die Alternative y wird von
einer Mehrheit der Individuen (A, C, D)
auch gegenüber dem Status quo
vorgezogen, und diese Mehrheit hat es in der
Hand, durch geschlossene Stimmabgabe ein Patt zu verhindern und die
Mehrheitsalternative y durchzusetzen. Für C ist es in dieser Konstellation rational, für y zu stimmen
und nicht für die eigentlich von ihm bevorzugte Alternative x.
Sofern eine Mehrheitsalternative existiert, die auch gegenüber dem Status quo von einer Mehrheit der Individuen vorgezogen wird, führt die Einfügung der Status-quo-Klausel also zur Durchsetzung dieser Mehrheitsalternative - immer vorausgesetzt, dass alle so abstimmen, dass das für sie vorteilhafteste Ergebnis herauskommt. Unter diesen Bedingungen ergibt sich aus der Klausel also keine Bevorzugung des Status quo gegenüber den andern Alternativen, und die bewusste Herbeiführung eines Patts kann nicht gelingen. Die Status-quo-Klausel verhindert also in diesem Fall eine erfolgreiche Obstruktion der Mehrheitsalternative.
Wenn es sich allerdings um eine Mehrheitsalternative handelt, die gegenüber dem Status quo keine Mehrheit hat, kann ein obstruktives Abstimmungsverhalten rational sein, wie das folgende Beispiel zeigt:
Präferenzordnungen
| A | B | C | D |
| y | z | x | y |
| z | (sq) | (sq) | (sq) |
| x | y | y | x |
| (sq) | x | z | z |
Abb.: 19.15
Hier hat y zwar gegenüber
x und z eine Mehrheit, aber nicht gegenüber - dem nicht zur Wahl gestellten - sq.
Wenn B jetzt zusammen mit C für x stimmt, so ergibt sich ein Patt wegen
Stimmengleichheit zwischen x und y. Damit wird der Status quo beibehalten, der
für beide Individuen besser ist als y. Insofern setzt sich eine scheinbar
vorhandene Mehrheitsalternative hier nicht durch. Der Grund liegt allerdings
darin, dass es sich nicht um eine Mehrheitsalternative gegenüber dem Status quo
handelt.
In diesem Fall führt die
Status-quo-Klausel zu einer Bevorzugung des Status quo gegenüber der Alternative y,
denn ein Paarvergleich zwischen beiden würde Stimmengleichheit ergeben.] Ende des Einschubs]
20. Kapitel
Abstimmungsstrategien isolierter Individuen
§ 121 Die spieltheoretische Analyse individueller
Abstimmungsstrategien durch FARQUHARSON
Auch wenn zwischen den Individuen keine
Abstimmungsvereinbarungen möglich sind, werden auf die Durchsetzung ihrer
Interessen bedachte Individuen bei Abstimmungen nicht unbedingt entsprechend
ihren tatsächlichen Präferenzen stimmen. Vor allem FARQUHARSON hat die
Abstimmungsstrategien analysiert, die isolierte Individuen bei Fehlen von
Koalitionsmöglichkeiten einschlagen können, um für sich ein vorteilhafteres
Ergebnis zu erzielen. [[1] Siehe FARQUHARSON 1969. Allerdings hat er vor allem
mehrstufige Abstimmungsverfahren analysiert, die hier nicht im Mittelpunkt der
Untersuchung stehen.]
Die Auswirkungen von strategischen Überlegungen isolierter
Individuen soll im Folgenden anhand der absoluten Mehrheitsregel mit
Status-quo-Klausel demonstriert werden.
Dabei sollen 3 Individuen A, B und C
über die 3 Alternativen x, y und z unter Berücksichtigung des Status quo
(symbolisiert durch 'sq') abstimmen, ohne dass Koalitionen möglich sind. Wenn man
wiederum Stimmenthaltungen ausschließt, so stehen den Individuen drei
Entscheidungsmöglichkeiten offen: sie können für x, y oder z stimmen. Diese drei
Abstimmungsstrategien sollen mit Sx, Sy und Sz symbolisiert werden.
Da es sich
hier um ein einstufiges {566} Wahlverfahren handelt, bei dem die Entscheidung in einem
Wahlgang fällt, besteht jede Strategie hier nur aus einer
Abstimmungsentscheidung. Bei mehrstufigen Wahlverfahren besteht eine
vollständige Abstimmungsstrategie aus den Entscheidungen zu allen Abstimmungen,
die im Laufe des Verfahrens möglich werden. [[2] Siehe dazu FARQUHARSON 1969, S.20f.]
Das Ergebnis der Abstimmung resultiert dann aus dem
Zusammentreffen der individuellen Abstimmungsstrategien. Zu jeder möglichen
Kombination von individuellen Abstimmungsstrategien kann man mit Hilfe der
angewandten Entscheidungs-Regel angeben, wie das dazugehörige Ergebnis lautet.
Nach der absoluten Mehrheitsregel mit Status-quo-Klausel gilt bei 3 Individuen
eine Alternative dann als kollektiv gewählt, wenn mindestens 2
Individuen für diese Alternative stimmen. Erhält keine der Alternativen die
absolute Mehrheit von 2 Stimmen, so gilt der Status quo als kollektiv
gewählt.
Da es sich in unserm Beispiel um 3 Individuen handelt, die
jeweils zwischen 3 Strategien wählen können, bestehen insgesamt 33 = 27
Strategiekombinationen. Die jeder möglichen Strategiekombination entsprechenden
kollektiven Entscheidungen zugunsten von x, y, z oder sq sind in der folgenden
drei-dimensionalen Tabelle wiedergegeben: {567}
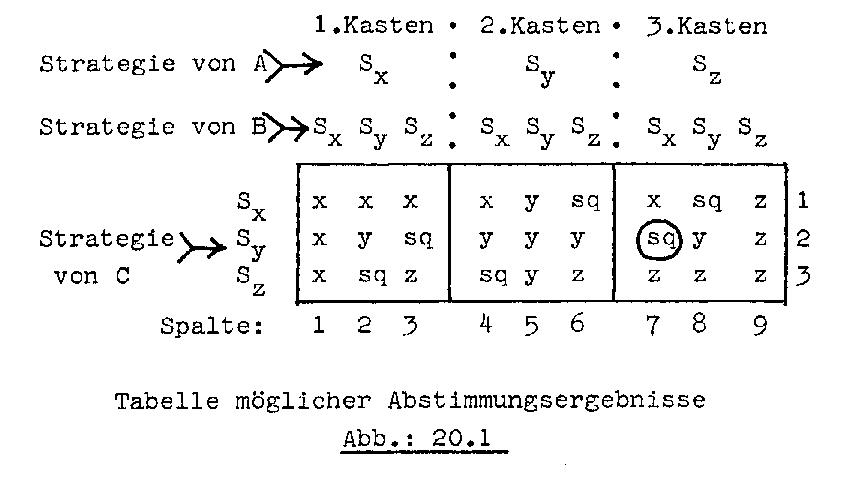
Die Tabelle aus Abb. 20.1 gibt z. B. an, welche kollektive
Entscheidung zustande kommt, wenn A für Sz, B für Sx und C für Sy sich entscheidet. Das Ergebnis hierfür
in Zeile 2, Spalte 7 lautet "sq" (in der Tabelle eingekreist).
Wenn man nun annimmt, dass es aufgrund von
Kommunikationsschwierigkeiten keine Möglichkeit zu Abstimmungsvereinbarungen
gibt, so steht jedes Individuum für sich vor dem Problem, wie es abstimmen soll,
um ein Abstimmungsergebnis zu erreichen, das seinen Interessen möglichst gut
entspricht. Dies Ziel wird ja keineswegs immer dadurch erreicht, dass das
Individuum 'aufrichtig" für seine Spitzenalternative stimmt. [[3] FARQUHARSON nennt ein Abstimmungsverhalten entsprechend
den tatsächlichen Präferenzen "sincere". S. dazu FARQUHARSON 1969, S.17f.]
{568}
Um das Problem isolierter individueller
Abstimmungsstrategien zu analysieren, seien die folgenden individuellen
Präferenzordnungen angenommen:
Präferenzordnungen
| A | B | C |
| x | y | z |
| sq | sq | y |
| y | z | x |
| z | x | sq |
Abb.: 20.2
Wenn bei dieser Interessenkonstellation Individuum C für seine Spitzenalternative z stimmt und die Strategie
Sz wählt, so kann das bei bestimmten Strategien der beiden andern Individuen für
C nachteilig sein.
Wenn z. B. A die Strategie Sx wählt und B die Strategie Sy -
symbolisiert durch (A: Sx / B: Sy) - so wäre die Strategie Sz für C nachteilig,
denn wie man in Zeile 3 / Spalte 2 der Abb. 20.1 sehen kann, wäre das Ergebnis
dann der Status quo, also das für C schlechteste aller möglichen Ergebnisse.
Hätte C dagegen bei dieser Strategiekombination der beiden andern Individuen die
Strategie Sy gewählt, so wäre das für C bessere Ergebnis y zustande gekommen.
Wenn in einer solchen Situation ohne
Kooperationsmöglichkeit ein Individuum die für sich vorteilhafteste Strategie
wählen will, so muss es möglichst wissen, welche Strategie die andern Individuen
wählen werden. Dies wäre nur in dem Fall unnötig, wenn für das Individuum eine
Strategie existiert, die bei allen möglichen Strategien der andern Individuen
mindestens ebenso gute Ergebnisse bringt wie irgendeine andere Strategie. [[4]
FARQUHARSON nennt eine solche Strategie "straightforward".
S. FARQUAHARSON 1969, S.30.]
In
unserm Beispiel existiert für {569} Individuum A eine solche unbedingt beste Strategie in Form
von Sx. Denn wenn man jedes einzelne Ergebnis des 1. Kastens mit den zugehörigen
Ergebnissen des 2. und 3. Kastens vergleicht, so sieht man,
dass jedes Ergebnis
des 1. Kastens für A mindestens ebenso gut ist wie das entsprechende Ergebnis
aus dem 2. oder 3. Kasten in Abb. 20.1. Das heißt, dass A bei gegebenen
Strategien von B und C mit den Strategien Sy oder Sz niemals ein besseres
Ergebnis erreichen kann als mit der Strategie Sx.
Für Individuum C existiert jedoch keine solche "unbedingt
beste" Strategie, wie man aus einem Vergleich der zusammengehörigen Felder in
den drei Zeilen ersehen kann. In jeder Zeile ist mindestens ein Ergebnis für C
schlechter als ein zugehöriges Ergebnis in einer der beiden andern Zeilen. Es
existiert also zu jeder möglichen Strategie von C eine andere Strategie, die
zumindest bei einer Strategiekombination der beiden andern Individuen zu einem
für C besseren Ergebnis geführt hätte, sodass keine Strategie für C als unbedingt
beste bezeichnet werden kann.
In einem solchen Fall muss Individuum C zu bestimmen
versuchen, welche Strategien die beiden andern Individuen wahrscheinlich wählen
werden, um dementsprechend die für sich vorteilhafteste Strategie zu bestimmen.
Wenn allerdings jedes Individuum so denkt, so könnte das zu einem Zirkel führen,
denn jeder kann seine eigene Strategie erst bestimmen, nachdem der andere seine
Strategie bestimmt hat, aber diesem geht es ebenso.{570}
§ 122 "Ausgeklügelte" individuelle Abstimmungsstrategien
Es gibt jedoch einen Ausweg aus diesem Dilemma, wie
FARQUHARSON nachweist. [[5] Siehe FARQUHARSON 1969, S.38f.] Wenn man davon ausgeht, dass Individuum C die
Präferenzordnungen bzw. die Interessenlage der übrigen Individuen kennt, so ist
die Bestimmung ihrer Strategien möglich, wenn man annimmt, dass
diese keine Strategien wählen werden, die für sie eher nachteilig sind. Ein
Individuum würde dann eine "unzulässige" (inadmissible) Strategie wählen, wenn
es eine andere Strategie gibt, die bei keiner möglichen Strategiekombination der
übrigen Individuen ein schlechteres Ergebnis und bei mindestens einer
Kombination ein besseres Ergebnis für das Individuum bringt. [[6] Siehe FARQUHARSON 1969,
S.28.]
Wie bereits oben ausgeführt wurde, sind in unserm Beispiel
für Individuum A die Strategien Sy und Sz "unzulässig" in diesem Sinne, denn Sx
bringt bei allen möglichen Strategiekombinationen der übrigen Individuen
zumindest gleich gute und in einigen Fällen sogar bessere Ergebnisse für A.
Insofern die andern Individuen davon ausgehen können, dass A unter diesen
Bedingungen die Strategie Sy wählen wird, wird damit der Bereich der möglichen
Ergebnisse schon auf den Kasten 1 eingeschränkt.
Für das Individuum B ist die Strategie Sz unzulässig, denn
die Strategie Sy bringt gegenüber Sz auf keinen Fall schlechtere Ergebnisse und
in einigen Fällen sogar bessere Ergebnisse, wie der Vergleich der Ergebnisse in
den Spalten 2, 5 und 8 mit den zugehörigen {571} Ergebnissen in den Spalten 3, 6 und 9 zeigt. Indem die
Strategie Sz als für B unzulässig ausgeschieden wird, wird der Bereich möglicher
Ergebnisse auf die Spalten 1, 2, 4, 5, 7 und 8 eingeschränkt.
Wenn Individuum C nun voraussetzt, dass A und B keine für
sie unzulässigen Strategien wählen werden, so werden für C in einer zweiten
Stufe ebenfalls bestimmte Strategien sekundär unzulässig. [[7] Zu den Stufen der "Zulässigkeit" von Strategien s. FARQUHARSON 1969, S.39.] Für
C kommen ja jetzt nur noch die Strategiekombinationen der Spalten 1 und 2 in
Frage, da für A nur die Strategie Sx und für B nur die Strategien Sx und Sy
zulässig sind.
Durch diese Eingrenzung der zu berücksichtigenden möglichen
Strategiekombinationen werden jetzt die Strategien Sx und Sz für C sekundär
unzulässig, denn die Strategie Sy bringt für C im Verhältnis dazu mindestens
gleich gute und teilweise bessere Ergebnisse, wie ein Vergleich der Ergebnisse
in Zeile 2 mit den zugehörigen Ergebnissen in Zeile 1 und 3 bezogen auf die
Spalten 1 und 2 zeigt. Für C bleibt also bei dieser Interessenkonstellation nur
Sy als zulässige Strategie.
Wenn Individuum B nun ebenfalls von der Annahme ausgeht,
dass A und C keine primär oder sekundär unzulässigen Strategien wählen werden, so
steht für B fest, mit welchen Abstimmungsstrategien es bei den übrigen
Individuen rechnen muss: A wird die Strategie Sx wählen und für x stimmen, und B
wird die Strategie Sy wählen und für y stimmen. Damit wird für B schließlich die
Strategie Sx tertiär unzulässig, da Sy für B jetzt mindestens ebenso gute
und {572} teilweise bessere Ergebnisse bringt als Sx, wie ein
Vergleich der Ergebnisse in Spalte 2 mit den entsprechenden Ergebnissen in
Spalte 1 und 3 bezogen auf die Zeile 2 des 1. Kastens zeigt. Damit bleibt für B
nur die Strategie Sy, also die Abstimmung für y, als zulässig übrig.
Es ist also allein aufgrund strategischer Überlegungen der
isolierten Individuen für jedes Individuum nur eine Strategie als zulässig übrig
geblieben. Diese Strategien ergeben die Strategiekombination (A: Sx / B: Sy / C: Sy), die als Ergebnis die kollektive Wahl der Alternative y haben.
[[8] Da es sich bei y um die Mehrheitsalternative handelt,
hätte sich y auch bei Möglichkeit der Koalitionsbildung durchgesetzt.]
Wenn die Individuen ihr Abstimmungsverhalten derart
strategisch durchdenken und bestimmen, so nennt FARQUHARSON ein solches Abstimmungsverhalten "ausgeklügelt" " (sophisticated) im Gegensatz zum "aufrichtigen" (sincere) Abstimmungsverhalten entsprechend
den tatsächlichen Präferenzen.[[9] S. dazu FARQUHARSON 1969, S.38ff. Die
Ergebnisse für "ausgeklügeltes" und "aufrichtiges" Abstimmungsverhalten bei
verschiedenen Wahlverfahren finden sich auf S.61ff.]
Wenn die Individuen ohne
Abstimmungsvereinbarungen mit anderen in dieser Weise ausgeklügelt abstimmen, um
ihre individuellen Interessen möglichst gut durchzusetzen, so stellt das
Endresultat der Abstimmung immer ein individuelles Gleichgewicht dar
oder, wie FARQUHARSON es auch ausdrückt, eine auf jedes einzelne Individuum
bezogen "unverletzliche" (invulnerable) Situation. Dabei gilt eine Situation
nach FARQUHARSON dann als {573} "verletzlich" in Bezug auf ein bestimmtes Individuum, wenn
eine andere Situation von diesem Individuum vorgezogen wird und wenn das
Individuum diese Situation allein durch eine Änderung seiner eigenen Strategie
herstellen kann. [[10] Siehe FARQUHARSON 1969, S.24 u. 51. Insofern stellt das
Resultat des ausgeklügelten Abstimmungsverhaltens natürlich nicht das einzige
individuelle Gleichgewicht in der Tabelle der Abb. 20.1 dar.]
Allerdings muss sich allein aufgrund des ausgeklügelten
Abstimmungsverhaltens der einzelnen Individuen nicht bei allen
Interessenkonstellationen eine einzige Strategiekombination als allein zulässig
für die Individuen herausschälen, wie es im vorigen Beispiel der Fall war. Dies
kann man anhand der folgenden Präferenzordnungen zeigen:
Präferenzordnungen
| A | B | C |
| x | y | z |
| sq | z | y |
| z | x | x |
| y | sq | sq |
Abb.: 20.3
Da wiederum 3 Individuen zwischen 3 Alternativen wählen
können und nach der absoluten Mehrheitsregel mit Status-quo-Klausel kollektiv
entschieden wird, gilt ebenfalls die Tabelle möglicher Ergebnisse aus Abb. 20.1.
Da Individuum A ähnliche Präferenzen hat wie im vorigen Beispiel, ist für A
wiederum die Strategie Sx die "unbedingt beste" und einzig zulässige Strategie.
Für B sind in diesem Fall jedoch alle 3 Strategien primär zulässig, wie
allein schon ein Vergleich der zugehörigen Ergebnisse der Spalten 1, 2 und 3
zeigt. Für C sind ebenfalls alle 3 {574} Strategien primär zulässig, wie ein Vergleich der Zeilen 1,
2 und 3 zeigt.
Auch unter der Annahme, dass A die für ihn unbedingt beste Strategie Sx wählt, lässt sich
der Bereich der zulässigen Strategien für B und C nicht weiter einschränken, sodass für
B und C
sämtliche 3 Strategien zulässig bleiben.
Allerdings lässt sich der Bereich der zu erwartenden
Strategiekombinationen auch innerhalb des 1. Kastens noch weiter einschränken,
da einige Strategiekombinationen zu Situationen führen, die für einzelne
Individuen "verletzlich" sind. Da verletzliche Situationen keine individuellen
Gleichgewichte darstellen, können sie auch nicht das Resultat eines "ausgeklügelten" Abstimmungsverhaltens der Individuen sein.
So kann Individuum C
bei der Strategiekombination (A: Sx / B: Sy / C: Sx) mit dem Ergebnis x durch
eine Änderung seiner Strategie nach Sy das für sich bessere Resultat y
durchsetzen.
Bei der Strategiekombination (A: Sx / B: Sz / C: Sx) mit dem
Ergebnis x kann C mit der geänderten Strategie Sz sogar statt x seine
Spitzenalternative z realisieren.
Bei der Kombination (A: Sx / B: Sx / C: Sz)
mit dem Ergebnis x könnte B mit der geänderten Strategie Sz die von ihm
gegenüber x vorgezogene Alternative z realisieren.
Damit konnten 4 weitere Strategiekombinationen
ausgeschlossen werden, aber mehr lassen sich aufgrund "ausgeklügelter"
Strategien der isolierten Individuen nicht eliminieren. Es bleiben sogar alle 4
möglichen Ergebnisse des Abstimmungsverfahrens, x, y, z und sq, weiterhin
möglich.
Bei dieser Interessenkonstellation und der vorausgesetzten
Entscheidungsregel ist das Ergebnis des Abstimmungsverfahrens strategisch also
nicht determiniert, wenn Abstimmungsvereinbarungen {575} zwischen den Individuen nicht möglich sind.
[[11] Sofern Koalitionsbildung möglich ist, wird sich dagegen
die Mehrheitsalternative z durchsetzen.]
§ 123 Möglichkeiten eines strategischen Dilemmas
Wie können in einem solchen Fall die Individuen B und C
verhindern, dass z. B. der von ihnen am wenigsten gewünschte Status quo das
Ergebnis des Abstimmungsverfahrens darstellt, und wie können sie erreichen, dass
die von ihnen bevorzugten Alternativen y und z durchgesetzt werden?
Wenn keine Kommunikation zwischen den Individuen über ihr beabsichtigtes
Abstimmungsverhalten möglich ist, so stellt sich das Problem für Individuum C z.
B. folgendermaßen dar:
Für C ist z die Spitzenalternative, die es am liebsten
realisiert sehen möchte. Dies setzt einmal voraus, dass es selber für z stimmt.
Zum andern muss jedoch auch B für z stimmen, damit z die absolute Mehrheit
erhält. Da für B jedoch nicht z sondern y die Spitzenalternative darstellt, kann
C nicht davon ausgehen, dass B für z stimmt. Für Individuum B stellt sich das
Dilemma ganz analog.
Wenn nun beide Individuen für ihre jeweilige
Spitzenalternative stimmen in der Erwartung, dass der andere schon nachgeben
werde und ebenfalls für diese - für ihn zweitbeste - Alternative stimmt, so
entsteht für beide Individuen das schlechteste der möglichen Ergebnisse, der Status quo.
Wenn die Individuen in dieser Situation "auf Nummer Sicher" gehen wollen, so
werden sie für die Alternative x stimmen, denn Sx ist für B und {576} C diejenige Strategie, die schlimmstenfalls die Alternative
x erbringen kann, während die beiden andern Strategien Sy bzw. Sz im schlimmsten
Fall sogar den am wenigsten gewünschten Status quo ergeben können.
Dies Dilemma ähnelt dem in der Spieltheorie bekannten "Gefangenen-Dilemma", einem Zwei-Personen-Spiel mit möglichen
Kooperationsvorteilen, die jedoch bei fehlender Kommunikation und der Annahme
eines "borniert" eigeninteressierten Verhaltens nicht wahrgenommen werden.
[[12] Siehe dazu z. B. LUCE/RAIFFA 1957, 5.94ff. oder RAPOPORT
1963, S.48ff.]
Anstelle einer "Maximin-Strategie" der Minimierung möglicher Verluste in Form
der Strategie Sy bestünde für isolierte Individuen außerdem noch die Möglichkeit einer "gemischten" Strategie, die aus
Lotterien über Strategien besteht, in unserm Beispiel also aus einer geeigneten
Zufallsauswahl aus den Strategien Sx, Sy und Sz. Der BERNOULLI-Nutzen einer
solchen gemischten Strategie kann dann u. U. höher liegen als der Nutzen der
Strategie Sx für das betreffende Individuum. [[13] Zum BERNOULLI-Nutzen s.o. § 41.] Allerdings muss auch durch solche
Zufalls-Strategien nicht unbedingt ein spieltheoretisches Gleichgewicht
hergestellt werden. [[14] Siehe
LUCE/RAIFFA 1957, S.9Off.]
In diesem Zusammenhang sind einige Überlegungen von LUCE
und RAIFFA dazu interessant, wie ein Individuum zwar ohne Kooperation aber
mithilfe gezielter einseitiger Kommunikation versuchen kann, seine
Spitzenalternative {577} durchzusetzen.
Wenn z. B. Individuum B von
vornherein ankündigt, dass es für y stimmen wird und dass keine Macht der Welt es
davon abbringen wird, so mag es für C - sofern es an die Entschlossenheit von B
zur Verwirklichung seiner Absicht glaubt - das beste sein, nun ebenfalls für y
zu stimmen. (Entsprechendes würde für B gelten, wenn C von vornherein erklärt,
dass es auf jeden Fall für z stimmen wird.) "Auf diese Weise sehen wir,
dass es in
einer solchen Situation vorteilhaft sein mag, die eigene Strategie als erster zu
enthüllen und für seine Starrköpfigkeit bekannt zu sein." [[15] LUCE/RAIFFA 1957, S.91.
Wie diese jedoch ausführen, kann
sich durch ein solches "starrsinniges" Vorgehen von B die Präferenzordnung von C
derart verändern, dass C aus Verärgerung über B jetzt lieber mit x vorlieb nimmt,
anstatt "klein beizugeben".]
§ 124 Unterschiede zwischen individuellen und kollektiven Abstimmungsstrategien
Wenn isolierte Individuen "ausgeklügelt" abstimmen, ohne
Abstimmungsvereinbarungen zu treffen, so ergeben sich individuelle
Gleichgewichtssituationen, die kein Individuum allein durch die Änderung seiner
eigenen Strategie zu seinen Gunsten verändern kann. Wenn man jedoch die
Möglichkeit von Abstimmungsvereinbarungen einbezieht, so ändert sich die
Sachlage entscheidend, und es kann zu völlig anderen Abstimmungsergebnissen
trotz Anwendung derselben Entscheidungs-Regel kommen. [[16] Spieltheoretisch
gesprochen handelt es sich um kooperative Spiele, die verbindliche
Vereinbarungen beinhalten. S. LUCE/RAIFFA
1957, S.89.]
Insofern können die
vorangegangenen Überlegungen über die Zulässigkeit von Strategien und über die
Verletzlichkeit von Situationen bzw. ihren Gleichgewichtscharakter nicht auf die
veränderte Problemlage übertragen werden. [[17] Da die Ergebnisse FARQUHARSONs sich auf ausgeklügelte
Abstimmungsstrategien nicht-kooperierender Individuen beziehen, sind ihre
Anwendungsmöglichkeiten sehr beschränkt. In der Abstimmungspraxis ist
Koalitionsbildung ja gewöhnlich möglich, und sie sollte im Interesse einer Durchsetzung der Mehrheitsalternative
auch immer zulässig sein.] {578}
Die kooperative Problemlage und die damit einhergehende
Veränderung der Lage kann anhand des Beispiels aus Abb. 20.3 veranschaulicht
werden. Wenn nämlich Abstimmungsvereinbarungen zugelassen werden, so ist
plötzlich für Individuum A die Strategie Sx gar nicht mehr die "unbedingt
beste", sondern A muss auch die Strategie Sz wieder in seine Überlegungen mit
einbeziehen.
Nehmen wir z. B. die Strategiekombination (A: Sx / B: Sy / C: Sy). In
dieser Situation würde das Ergebnis y realisiert, das für A die schlechteste
aller möglichen Alternativen bildet. A könnte allein durch eine Änderung
seiner eigenen Strategie kein für sich besseres Ergebnis erzielen, denn die zwei
Stimmen von B und C für die Alternative y würden in jedem Fall den Ausschlag für
y geben.
In gleicher Weise gäbe es auch für B oder C bei dieser
Strategiekombination keine Möglichkeit, allein durch eine Änderung ihrer eigenen
Strategie ein für sich vorteilhafteres Ergebnis zu erzielen. Wenn Individuum C
z. B. seine Spitzenalternative z wählen würde, so wäre das Resultat der Status
quo, also noch schlechter als y. Es handelt sich bei dieser Strategiekombination
also um ein individuelles Gleichgewicht. {579}
Wenn man jedoch Abstimmungsvereinbarungen zwischen den
Individuen zulässt, so kann es für A bei der Strategiekombination (A: Sx / B: Sy /
C: Sy) vorteilhaft sein, die Strategie Sz zu wählen, und zwar unter der
Bedingung, dass auch C die Strategie Sz wählt. Durch eine solche
Abstimmungsvereinbarung zwischen A und C auf der Basis von Sz würde mit der
Alternative z ein Ergebnis herauskommen, das für beide besser ist als das
vorherige Ergebnis y. In dieser kooperativen Situation ist also Sx für Individuum A nicht mehr die unbedingt beste Strategie.
Dieser Wandel entsteht dadurch,
dass in der nicht-kooperativen Situation jedes Individuum bei der Bestimmung
seiner eigenen Strategie die Strategien der andern Individuen als gegeben
ansehen muss und sich nur fragt, ob sich durch die Veränderung seiner eigenen
Strategie in jedem Fall mindestens ebenso gute und in einigen Fällen sogar
bessere Ergebnisse erzielen lassen. Jetzt müssen dagegen die Strategien einer
absoluten Mehrheit von Individuen variiert werden, um zu sehen, ob sich für
jedes der beteiligten Individuen durch eine gemeinsame Abstimmungsstrategie ein
gleich gutes oder besseres Resultat erzielen lässt.
Im Rahmen eines absoluten Mehrheitssystems mit
Koalitionsmöglichkeit ist jetzt jede Situation "verletzlich", wenn es eine
andere Situation gibt, deren Ergebnis von einer absoluten Mehrheit der
Individuen vorgezogen wird. Eine Situation kann dementsprechend nur dann ein
Gleichgewicht in Bezug auf eine absolute Mehrheit von Individuen darstellen,
wenn es nicht in Bezug auf eine absolute Mehrheit verletzlich ist. [[18] S. dazu die Ausführungen von FARQUHARSON
1969, S.50ff.] {580}
FARQUHARSON klassifiziert die Gleichgewichte entsprechend
der Zahl der Individuen, für die die Situation nicht verletzlich sein darf: "Eine Situation ist ein Gleichgewicht der Ordnung r, wenn es nicht verletzlich
ist in Bezug auf irgendeine Menge von r Abstimmenden. ... Eine Situation, die ein
Gleichgewicht aller Ordnungen von 1 bis n (der Gesamtzahl der Abstimmenden, E.W.) ist, nennen wir ein kollektives Gleichgewicht."
[[19] FARQUHARSON 1969, S.51f.] FARQUHARSON weist dabei
darauf hin, "dass ein Gleichgewicht der Ordnung 1 nicht notwendig ein
Gleichgewicht irgendeiner höheren Ordnung sein muss und dass auch nicht die
Umkehrung gilt. [[20] FARQUHARSON 1969, S.51.]
So bildet z. B. die Strategiekombination (A: Sx / B: Sy / C:
Sy) mit dem Ergebnis y in dem Beispiel aus Abb. 20.3 ein individuelles
Gleichgewicht aber kein Gleichgewicht in Bezug auf zwei Individuen, wie oben
gezeigt wurde.
Umgekehrt bildet die Strategiekombination (A: Sz / B: Sy / C: Sz)
mit dem Ergebnis z zwar kein individuelles Gleichgewicht, denn Individuum A
könnte durch eine Änderung seiner Strategie nach Sx das für sich günstigere
Resultat des Status quo realisieren, aber dennoch handelt es sich dabei um ein
Gleichgewicht in Bezug auf eine absolute Mehrheit von zwei Individuen, denn es
gibt bei dieser Strategiekombination keine absolute Mehrheit von zwei
Individuen, die durch eine gemeinsame Änderung ihrer Abstimmungsstrategien eine
Verbesserung des Ergebnisses für sich erzielen könnten. {581}
Daraus ergibt sich, dass sich in Abstimmungsverfahren bei
Anwendung der gleichen Entscheidungs-Regel unterschiedliche Ergebnisse
herausbilden können, je nachdem, ob Abstimmungsvereinbarungen möglich sind oder
nicht. Nur in den Fällen, wo Koalitionsbildung dieser Art nicht möglich ist,
sind FARQUNARSONs Ergebnisse über individuell "ausgeklügeltes"
Abstimmungsverhalten anwendbar. [[21] Zwischen den beiden Extremen "überhaupt keine
Koalitionsbildung" und "vollkommene Koalitionsbildung" kann es jedoch noch eine
Reihe von Zwischenformen geben, etwa wenn für bestimmte Individuen einige andere
Individuen koalitionsfähig sind und andere dagegen nicht. Ein Beispiel dafür ist
die Mehrheitsbildung in einigen westeuropäischen Parlamenten, wo die
Kommunistischen Parteien nicht koalitionsfähig für die andern Parteien sind. In
solchen Fällen beschränkter Koalitionsmöglichkeiten sind jeweils spezielle
Analysen erforderlich. Siehe hierzu z. B. den Versuch, solche "Regeln zulässiger
Koalitionswechsel" zu berücksichtigen, bei LUCE/RAIFFA 1957, S.166ff. sowie die
Untersuchung verschiedener Koalitionstheorien bei FACH 1974.]{582}
21. Kapitel
Abstimmungsstrategien bei Serien von Entscheidungen im Mehrheitssystem
§ 125 Der
Stimmentausch
In den vorangegangenen Kapiteln wurde die Anwendung des
Mehrheitsprinzips auf einzelne Entscheidungen untersucht. Wie gezeigt wurde,
führt das eigeninteressierte Abstimmungsverhalten der Individuen dazu, dass sie
nicht unbedingt für die von ihnen am meisten gewünschte Alternative stimmen.
Dieser Einfluss strategischer Erwägungen wird nun noch verstärkt, wenn es nicht
um einzelne, isolierte Entscheidungen geht, sondern wenn ganze Entscheidungsserien nach dem Mehrheitsprinzip entschieden werden. Dabei kann es zu
Abstimmungsvereinbarungen kommen, die mehrere Entscheidungen gleichzeitig
umfassen und ganze Alternativenbündel zur Grundlage haben. Da in der Praxis
des Mehrheitssystems gewöhnlich nicht nur eine Entscheidung sondern mehrere
Entscheidungen überschaubar sind, kommt der Untersuchung dieses Aspektes eine
besondere Bedeutung zu.
Eine Möglichkeit für die Individuen, bei
Entscheidungsserien die Abstimmungsergebnisse zu ihren Gunsten zu beeinflussen,
ist der Stimmentausch, bei dem die Individuen ihre Stimme bei einer
ihnen weniger wichtigen Entscheidung austauschen gegen eine {583} Stimme bei einer ihnen wichtigeren Entscheidung.
[[1] Zum Stimmentausch (englisch "log-rolling" ) s.
BUCHANAN/TULLOCK 1969, S.121ff. Zum Stimmentausch in Einstimmigkeits-Systemen
s.o. § 73.]
Die Auswirkungen des Stimmentauschs können an einem
Beispiel verdeutlicht werden. Dabei stimmen 3 Individuen A, B und C in der
Entscheidung I zwischen den Alternativen x und y und in der Entscheidung II
zwischen den Alternativen w und z ab. Dabei sollen die intrasubjektiven
Präferenzintensitäten in der Tabelle durch die Abstände zwischen den
Alternativen ausgedrückt werden.
Entscheidung I Entscheidung II
Präferenzordnungen (mit intrasubjektiven Intensitäten)
| A | B | C | A | B | C | ||
| x | y | y | w | z | w | ||
| - | x | - | z | - | - | ||
| - | - | x | - | - | z | ||
| y | - | - | - | w | - |
Abb.: 21.1 Abb.: 21.2
Individuum A hat also bei der Entscheidung I eine sehr viel
stärkere Präferenzintensität für x gegenüber y als bei der Entscheidung II für w
gegenüber z. Dies bedeutet, dass für A die Entscheidung I sehr viel wichtiger ist
als die Entscheidung II, denn die Entscheidung I kann sein Nutzenniveau in sehr
viel stärkerem Maße verändern als die Entscheidung II.
Bei dem Individuum B ist die Situation genau umgekehrt. Für
B ist die Entscheidung II wichtiger als die Entscheidung I, denn die
Nutzenspannweite zwischen {584} der besten und der schlechtesten Alternative ist bei
der Entscheidung II sehr viel größer. Dagegen ist das Individuum C von beiden
Entscheidungen gleich stark betroffen, denn seine Präferenzintensität ist bei I
und II gleich. [[2] Die Präferenzintensitäten müssen dabei nicht notwendig interpersonal vergleichbar sein, denn es muss für den Tausch ja nur
jedes Individuum seine eigenen Präferenzintensitäten miteinander vergleichen.]
Bei einer isolierten Abstimmung über jede einzelne Entscheidung würden sich bei Anwendung der relativen Mehrheitsregel folgende Entscheidungen ergeben:
Entscheidung I Entscheidung II
Wahlmatrix zu 22.1 Wahlmatrix zu 22.2
| x | y | w | z | ||||
| x | - | 1:2 | w | - | 2:1 | ||
| y | 2:1 | - | z | 1:2 | - |
Abb.: 21.3 Abb.: 21.4
Bei Anwendung der relativen Mehrheitsregel auf die
isolierten Entscheidungen, also ohne dass die Individuen einen Zusammenhang
zwischen den Entscheidungen herstellen können, würden die Alternativen y und w
erfolgreich sein.
Wenn jedoch zwischen den Individuen A und B ein für beide
Seiten vorteilhafter Stimmentausch stattfindet, sodass A bei Entscheidung I und B
bei Entscheidung II praktisch jeweils zwei Stimmen zur Verfügung haben, so
ergibt sich ein völliges anderes Ergebnis. {585}
Entscheidung I
Entscheidung II
nach Stimmentausch zwischen A und B
Wahlmatrix Wahlmatrix
| x | y | w | z | ||||
| x | - | 2:1 | w | - | 1:2 | ||
| y | 1:2 | - | z | 2:1 | - |
Abb.: 21.5 Abb.: 21.6
Bei einem Stimmentausch zwischen A und B ergeben sich also
mit x und z völlig andere Mehrheiten als bei der isolierten Abstimmung.
Wie man sieht, üben beim Stimmentausch die intrasubjektiven
Präferenzintensitäten der Individuen einen Einfluss auf das Abstimmungsergebnis
aus, sodass die einfachen ordinalen Präferenzordnungen zu den
Einzelentscheidungen zur Bestimmung des Ergebnisses nicht ausreichen.
Vom
Gesichtspunkt des Pareto-Kriteriums her gesehen ist ein solcher Stimmentausch
positiv zu bewerten, denn wie TULLOCK ausführt, führt er zu Ergebnissen, die paretomäßig besser sind als die Ergebnisse isolierter Abstimmungen. "In einem
System, wo Stimmentausch nicht erlaubt ist, gibt der Wähler einfach seine
Präferenz an, und die Präferenz der Mehrheit der Wähler wird ausgeführt. Der
Defekt - und es ist ein ernster - dieses Verfahrens besteht darin, dass es die
verschiedenen Intensitäten der Wählerwünsche ignoriert. Jemand, der
leidenschaftlich gegen eine Maßnahme eingestellt ist, und jemand, dem diese
nicht viel ausmacht aber der sie leicht bevorzugt, werden gleich gewichtet.
Offensichtlich könnten beide sehr leicht besser gestellt werden, wenn es
demjenigen, der stark betroffen ist, erlaubt wäre, dem andern, der eine schwache
Präferenz hat, ein Geschenk {586} zu machen zum Ausgleich für eine Änderung seiner
Entscheidung. Die Befriedigung beider würde verbessert und die sich ergebende
Situation würde unter streng paretianischem Gesichtspunkt dem Ergebnis einer
Wahl mit gleicher Gewichtung der Stimmen überlegen sein." [[3] TULLOCK
1959, S.170]
Zu dieser Auffassung TULLOCKs sind jedoch eine Reihe
kritischer Anmerkungen erforderlich.
Zum einen muss scharf unterschieden werden
zwischen einem Stimmentausch im eigentlichen Sinne und einem Stimmenkauf
durch andere Gegenleistungen als ein bestimmtes Abstimmungsverhalten. Wenn
Stimmen durch "Geldgeschenke" gekauft werden können, so werden sich diejenigen
Individuen mit dem größeren Vermögen auch bei Abstimmungen stärker durchsetzen
können. Und je ungleicher das Eigentum in einer Gesellschaft verteilt ist, umso
weniger kann die Zahlungsbereitschaft eines Individuums für die Stimme in einer
Entscheidung als ein Ausdruck seiner interpersonal vergleichbaren
Präferenzintensität genommen werden, wie oben bei der Diskussion des Geldes als
Nutzenmaßstab bereits dargelegt wurde. [[4] Siehe oben § 45.]
Durch Stimmenkauf verliert das
Mehrheitssystem die Eigenschaft der Gleichgewichtung der individuellen
Präferenzordnungen und gleicht sich in der Gewichtung der bestehenden Verteilung
des Eigentums an. Stimmenkauf ist dabei zusätzlich unakzeptabel in
repräsentativen Gremien und wird hier zur den Gesamtwillen bewusst verfälschenden
{587} Bestechung, da durch Zahlungen an den Repräsentanten ohne
entsprechende Zahlungen an die Repräsentierten gezielt eine Interessendivergenz geschaffen wird, die einer Interessenvertretung entgegensteht.
Aber selbst wenn man einen echten Stimmentausch betrachtet,
so stimmt es nicht, dass das Ergebnis nach Stimmentausch "unter streng paretianischem Gesichtspunkt" besser geworden ist, wie TULLOCK meint. Dies kann
an dem obigen Beispiel verdeutlicht werden. Ohne Stimmentausch zwischen A und B
fiel die kollektive Entscheidung auf die Alternativen y und w, wie aus den Abb.
21.3 und 21.4 hervorgeht. Nach dem Stimmentausch siegten dagegen die
Alternativen x und z.
Wenn es sich um eine streng paretianische Verbesserung
dabei handeln soll, so müssen alle Individuen die Ergebnisse x und z gegenüber y
und w vorziehen oder müssen sie zumindest gleich gut finden. Wie man sofort
sieht, gilt dies jedoch nicht für das Individuum C, dessen Spitzenalternativen y
und w ohne Stimmentausch siegten, aber nach dem Stimmentausch unterlagen.
Individuum C wird also durch den Stimmentausch zwischen A und B bei beiden
Entscheidungen schlechter gestellt, sodass von einer paretomäßigen Verbesserung
des Abstimmungsergebnisses eigentlich nicht die Rede sein kann.
Um von einer paretomäßigen Verbesserung durch Stimmentausch
sprechen zu können, muss man die Betrachtung auf die an der Vereinbarung des
Stimmentausches beteiligten Individuen einschränken. Die Stimmabgabe wird dazu
dem Verfügungsbereich des jeweiligen Individuums zugeteilt und mögliche "externe
Effekte" auf Dritte werden unberücksichtigt gelassen, ähnlich wie {588} im Eigentum-Vertrags-System.
[[5] Siehe oben Kap. 14.] Nur wenn man die interessemäßigen Interdependenzen zwischen dem Abstimmungsverhalten der
Individuen ausdrücklich ignoriert, kann man von paretomäßigen Verbesserungen
durch Stimmentausch sprechen.
Festgehalten sei außerdem noch, dass TULLOCK in dem obigen
Zitat nicht den Unterschied zwischen der Berücksichtigung der intrapersonalen
und der interpersonalen Präferenzintensitäten macht. Eine Berücksichtigung der interpersonal vergleichbaren Nutzendifferenzen wäre unter dem Gesichtspunkt
einer solidarischen Bestimmung des Gesamtnutzens außerordentlich wichtig, wie
oben in § 37 ausgeführt wurde.
Durch einen Stimmentausch kann jedoch nur eine
Berücksichtigung der intrapersonal vergleichbaren Nutzendifferenzen erzielt
werden. Denn ein stattgefundener Stimmentausch lässt nur den Schluss zu, dass den
beteiligten Individuen die eine Entscheidung wichtiger war als die andere. Ein interpersonaler Nutzenvergleich findet dabei also nicht statt. Insofern kann
der "ernste Defekt" des Mehrheitssystems in Form einer mangelnden
Berücksichtigung der interpersonal vergleichbaren Präferenzintensitäten, den
TULLOCK durch sein Beispiel verdeutlicht, durch den Mechanismus des
Stimmentauschs noch nicht behoben werden, wie es bei TULLOCK den Anschein hat.
[[6] Zur Berücksichtigung interpersonal vergleichbarer
Präferenzintensitäten s.u. § 138 und Kap. 23.] {589}
Der Stimmentausch zwischen bestimmten Individuen hat
ähnliche Auswirkungen auf das Abstimmungsergebnis wie eine Zusammenfassung der
Einzelentscheidungen zu einer Gesamtentscheidung und eine entsprechende
Bündelung der Einzelalternativen. Das Ergebnis nach Stimmentausch zwischen A und
B im obigen Beispiel ist dasselbe, als wenn die Entscheidungen I und II zu einer
Gesamtentscheidung über die Alternativenbündel "x mit z" und "y mit w"
zusammengefasst werden. Die Präferenzordnungen der drei Individuen hinsichtlich
dieser beiden Alternativenbündel lassen sich durch die folgende Tabelle
wiedergeben:
Präferenzordnungen (zu Alternativenbündeln)
| A | B | C |
| x+z | x+z | y+w |
| y+w | y+w | x+z |
Abb.: 21.7
Die Wahlmatrix zu dieser Präferenzordnung sieht dann
folgendermaßen aus:
Wahlmatrix zu Abb.21.7
| x+z | y+w | |
| x+z | - | 2:1 |
| y+w | 1:2 | - |
Abb.: 21.8
Im Falle einer derartigen Bündelung der Alternativen hätten
also die Individuen A und B für "x mit z" gestimmt. Für A wäre die Realisierung
von x vorrangig gewesen und es hätte dafür z "in Kauf genommen". Für B wäre
umgekehrt die Realisierung von z vorrangig gewesen, und es hätte dafür x in Kauf
genommen. Individuum C hätte für die Alternative "y mit w" gestimmt, sodass sich
mit x und z bei der Gesamtentscheidung dieselben Alternativen durchsetzen wie
bei getrennten Abstimmungen mit Stimmentausch zwischen A und B. {590}
Wie man sieht, hat die Art der Bündelung oder Aufspaltung
der Alternativen bei Mehrheitsabstimmungen einen erheblichen Einfluss auf das
Ergebnis. Dadurch wird die Wichtigkeit derjenigen Verfahren unterstrichen, die
die Formulierung der Alternativen und ihre Aufstellung zur Entscheidung regeln.
Problematisch wäre unter diesem Gesichtspunkt etwa ein Verfahren, wie es
gelegentlich bei Volksabstimmungen bzw. Referenden angewandt wird, wo die
Initiative zur Abstimmung und die Formulierung der Alternativen ausschließlich
einer Instanz vorbehalten bleibt, die selber Partei im Konflikt ist, z. B. der
Regierung.
Falls diese Instanz keine Mehrheit für die eigene Spitzenalternative erwartet,
wird sie überhaupt kein Referendum
durchführen. Wenn sie aber eines durchführt, so wird sie solche
Alternativenbündel formulieren, dass sie mit einer Mehrheit der Stimmen rechnen
kann. Unter diesen Bedingungen kann natürlich nicht von einer Anwendung des
Mehrheitsprinzips die Rede sein, weil es parteiischer Willkür überlassen
bleibt, welche Entscheidungen überhaupt per Abstimmung entschieden werden und
welche Probleme anderweitig entschieden werden. Die Abstimmung hat in diesem
Fall nur eine reine Akklamationsfunktion.
§ 126 Stimmentausch oder Koalitionsbildung?
Im vorangegangenen Paragraphen wurde die Möglichkeit eines
für die Beteiligten vorteilhaften zweiseitigen Stimmentauschs dargestellt. Wie
im Folgenden näher begründet wird, handelt es sich jedoch bei
Abstimmungsvereinbarungen zu Serien von Einzelentscheidungen nicht
notwendigerweise um einen {591} Stimmentausch. Eine Stimme gegen eine andere auszutauschen,
heißt ja genaugenommen, dass jeweils ein Individuum dem andern seine Stimme bei
einer Entscheidung wechselseitig überlässt, sodass der andere frei über diese
Stimme verfügen kann. Dabei bleiben beide Individuen ansonsten völlig unabhängig
und verfolgen mit den "erworbenen" Stimmen selbständig ihre eigenen Interessen.
Ein solcher regelrechter Stimmenhandel nutzt die
Möglichkeit von Abstimmungsvereinbarungen zum Vorteil aller Beteiligten jedoch
nur zum Teil aus. Denn oft sind die Individuen an allen Entscheidungen - wenn
auch unterschiedlich stark - interessiert, sodass es ihnen nicht gleichgültig
sein kann, wie die von ihnen abgetretene Stimme durch den andern eingesetzt
wird. So mag für ein Individuum die Spitzenalternative des andern
völlig unakzeptabel sein, aber es wäre bereit, dessen zweitbeste Alternative zu
unterstützen. Zur Realisierung einer Abstimmungsvereinbarung darüber wäre ein
regelrechter Stimmentausch jedoch ungeeignet. Dazu bedarf es der Bildung einer
Koalition in Form eines Stimmenfonds, in den alle Individuen, die sich davon
Vorteile versprechen, ihre Stimmen einbringen und der nach einem für alle
Koalitionsmitglieder verbindlichen Plan eingesetzt wird. Eine solche
Koalitionsbildung war bereits bei Einzelentscheidungen analysiert worden und
bezieht sich bei Koalitionen zu Entscheidungsserien nicht auf Einzelalternativen
sondern immer auf ganze Alternativenbündel.
Insofern bei Koalitionen ein gemeinsam eingesetzter
Stimmenfonds gebildet wird, erscheint eine Charakterisierung der
Koalitionsbildung im Mehrheitssystem {592} als "stillschweigender Stimmentausch" (implicit logrolling)
durch TULLOCK als unzutreffend. [[7] Vgl. TULLOCK 1959, S.170.] Die Analogie zur Koalitionsbildung im
Mehrheitssystem wäre im Eigentum-Vertrags-System eigentlich nicht der Tausch
von Gütern, sondern eigentumsmäßige Kooperation von Individuen, die ihr
individuelles Eigentum in einen gemeinsam verwalteten Fonds einbringen, um
daraus Vorteile produktiver oder konsumptiver Art zu ziehen. [[8] Dieser wichtige Bereich vertraglicher Aktivitäten war in
der obigen Analyse des Eigentum-Vertrags-Systems ausgeklammert worden.]
§ 127 Probleme eines "marktmäßigen" Stimmentauschs und die Vorteile von Abstimmungskoalitionen
Es gibt eine ganze Reihe von Gründen, warum ein in der Form
eines Marktes organisierter Stimmentausch nicht funktionieren kann und
stattdessen Koalitionsbildung stattfindet. Als einer der Gründe hierfür war bereits
genannt worden, dass der echte Stimmentausch nur einen Teil der insgesamt
möglichen vorteilhaften Vereinbarungen abdecken kann.
Ein weiterer Grund sind die gewaltigen Verhandlungskosten, die auf jedes Individuum
zukommen, das im Rahmen eines größeren Kollektivs versucht, als individueller
Anbieter und Nachfrager von Stimmen eine Mehrheit bei den ihm selber wichtigsten
Entscheidungen zusammenzubringen. Es müsste dazu zahlreiche - oft genug
vergebliche - Verhandlungen führen, und bei terminierten Abstimmungen {593} wird dazu oft die verfügbare Zeit überhaupt nicht
ausreichen. Insofern ist regelrechter Stimmentausch eigentlich nur in
kleineren, überschaubaren Gremien denkbar.
Außerdem besäße ein einzelnes Individuum bei größeren
Kollektiven wahrscheinlich nicht genügend "Stimmkraft", um auch nur bei einer
einzigen Entscheidung allein die erforderliche Stimmenmehrheit auf dem Wege des
Tausches zusammenzubringen. Ökonomisch gesprochen sind die Alternativen "unteilbare Güter", insofern sie entweder angenommen oder abgelehnt werden. Ein
Individuum, dessen Stimmkraft für eine Mehrheit nicht ausreicht, kann in diesem
Fall also nicht versuchen, mit seinen Stimmen die Alternative zumindest
teilweise durchzusetzen. Im Mehrheitssystem gilt in Bezug auf eine bestimmte
Alternative ein Alles-oder-Nichts-Gesetz, anders als bei normalen Gütern im
Tausch-System, wo ein Individuum mit geringerer Kaufkraft eben entsprechend
weniger von einem Gut erwerben kann.
Wenn es sich z. B. um ein Kollektiv von 1 Million
abstimmenden Individuen handelt, das nach der absoluten Mehrheitsregel 100
Entscheidungen zu treffen hat, so müsste das Individuum versuchen, bei der ihm
wichtigen Entscheidung 500 000 Stimmen zusammenzubringen im Austausch gegen
höchstens 99 Stimmen zu den übrigen Einzelentscheidungen. Dies würde sicherlich
seine Stimmkraft übersteigen. Ein regelrechter Stimmenmarkt kann also bei
größeren Kollektiven nicht funktionieren, wie auch TULLOCK feststellt: "Der
Wähler kann seine Stimme bei der einen Entscheidung nicht für Stimmen bei
anderen Entscheidungen austauschen, weil er und seine Bekannten einen zu kleinen
{594} Teil der Gesamtwählerschaft ausmachen, um noch die
damit verbundenen Anstrengungen wert zu sein." [[9] TULLOCK 1959, S.170.]
Außerdem treten beim regelrechten Stimmentausch die
Probleme des Naturaltausches wieder auf, denn um einen solchen handelt es sich
ja, wenn die Stimme bei der einen Entscheidung gegen die Stimme bei der andern
Entscheidung ausgetauscht wird. Die eine Stimme kann dabei den dreifachen
Tauschwert der anderen haben, sodass ihr Austausch problematisch ist. Und die
Einführung eines generellen Tauschmittels wie Geld lässt sich insofern nicht
realisieren, als sich Stimmen zu bestimmten Entscheidungen nicht aufbewahren
lassen, sondern mit der Durchführung dieser Entscheidung verfallen. [[10] Zur Aufhebung dieser Problematik müsste ein
völlig verändertes Entscheidungssystem mit
aufhebbaren, teilbaren, für alle Entscheidungen anwendbaren "Stimmmarken" konstruiert werden. Zum Naturaltausch
s. § 88.]
Als weitere institutionelle Voraussetzung des
Stimmentauschs, die allerdings in gleicher Weise für die Bildung von
Abstimmungskoalitionen gilt, nennt TULLOCK die offene Abstimmung: "Die Anwendung
der geheimen Abstimmung macht es unmöglich zu sagen, ob
Abstimmungsvereinbarungen eingehalten wurden." [[11] TULLOCK 1959, S.170.]
In Bezug auf Koalitionen kann
diese Problematik jedoch durch die Anwendung zweistufiger Repräsentativverfahren
gemildert werden, wo der Repräsentant geheim gewählt wird und dann die hinter
ihm stehende Koalition von Individuen notwendigerweise geschlossen
repräsentiert.{595}
Ein entscheidendes Hindernis für einen atomistischen
Stimmenmarkt ist immer dann gegeben, wenn ein Teil der Entscheidungen die
Interessen vieler Individuen berührt, wenn es dabei also ökonomisch gesprochen
nicht um private sondern um kollektive bzw. öffentliche Güter geht.
Die Durchsetzung einer
kollektiv interessierenden Alternative bringt automatisch vielen Individuen
Vorteile (oder Nachteile), gleichgültig ob sie sich mittels Stimmentausch um das
Zustandekommen der Mehrheit bemüht haben oder nicht. In einer solchen Situation,
wo einerseits der Nutzen einer durchgesetzten Alternative kollektiv anfällt und
von ihm niemand ausgeschlossen werden kann und wo andererseits die Kosten der
Durchsetzung individuell anfallen, neigen auf ihren eigenen Vorteil bedachte
Individuen zum "Trittbrett-Fahrer-Verhalten". [[12] Zu öffentlichen Gütern und Trittbrett-Fahrer-Verhalten s.o. § 92.]
Das heißt, dass Individuen die
Vorteile bestimmter Alternativen mitnehmen, ohne sich an den Kosten ihrer
Durchsetzung zu beteiligen. Ein Individuum steht sich in einem solchen Fall
besser, wenn sich die andern Individuen um Mehrheiten für die kollektiv
vorteilhaften Alternativen bemühen und dafür ihre Stimmkraft opfern, indem sie
auf dem Wege des Stimmentauschs Stimmen sammeln. Gleichzeitig spart es selber
seine Stimmkraft auf und konzentriert sie auf diejenigen Alternativen, die
vorwiegend ihm selber Vorteile verschaffen, also eher private Güter betreffen.
Durch ein solches Trittbrett-Fahrer-Verhalten profitiert das Individuum bei den
eher öffentliche Güter betreffenden Entscheidungen von den Anstrengungen der
andern, während es sich zusätzlich private Vorteile verschafft durch
Konzentration seiner {596} ganzen Stimmkraft auf die vorwiegend nur es selbst betreffenden Entscheidungen. Im Rahmen eines Stimmenmarktes besteht deshalb die
Tendenz, dass gerade für Alternativen mit eher allgemeinem bzw. kollektivem
Nutzen keine Mehrheiten zustande kommen, da jeder gern die andern "die Kastanien
aus dem Feuer holen lässt".
Wenn sich jedoch alle Individuen einer gleichartig
interessierten Gruppe in dieser Weise als Trittbrett-Fahrer verhalten, so gibt
es - um im Bilde zu bleiben - niemanden mehr, der den gemeinsamen Wagen
vorwärtsbringt und für die erforderliche Stimmenmehrheit sorgt, indem er Stimmen
zu andern Entscheidungen dafür im Austausch opfert. Dadurch "fahren" die
Individuen im Endergebnis schlechter, als wenn sie alle einen bestimmten Teil
ihrer Stimmkraft für die kollektiv interessierenden Alternativen eingesetzt
hätten. Ein Stimmenmarkt kann jedoch ein derartiges verbindliches Vorgehen nicht
garantieren. Das Versagen des Marktmechanismus im Falle öffentlicher Güter
wiederholt sich also beim Stimmenmarkt im Mehrheitssystem, sofern Individuen vom
Nutzen einiger Alternativen nicht ausgeschlossen werden können.
Ein weiterer Grund für das Versagen eines Stimmenmarktes
liegt darin, dass die isoliert voneinander agierenden Individuen nur schwerlich
Informationen darüber besitzen können, ob für eine bestimmte Alternative bereits
die erforderliche Stimmenzahl erreicht ist oder nicht. Werden nämlich über das
erforderliche Maß hinaus weitere Stimmen im Austausch erworben, so sind die
dafür hergegebenen Stimmen vergeudet, da es keinerlei Einfluss auf das Ergebnis
hat, wie groß die Mehrheit gewesen ist.{597}
Wird andererseits die erforderliche Stimmenmehrheit nicht
erreicht, so sind alle dafür eingesetzten Stimmen vergeudet worden, denn die
Stimmen der Minderheit gehen im Mehrheitssystem ja verloren. Dies ist anders
als auf einem regelrechten Geldmarkt, wo der unterlegene Bieter zwar das Gut
nicht erhält, das an den Meistbietenden geht, wo er aber andererseits auch das
Geld, das er vergeblich geboten hat, behalten darf. Für isolierte Individuen ist
es aber außerordentlich schwierig, die Erfolgsaussichten einer Alternative und
die zur Mehrheit noch erforderlichen Stimmen zuverlässig abzuschätzen, sodass ein
Stimmenmarkt auch in dieser Hinsicht nicht als praktikabel erscheint.
Als letztes ist noch zu berücksichtigen, dass häufig gar
nicht von vornherein genau feststeht, welche Entscheidungen mit welchen
Alternativen zukünftig zu treffen sein werden. Wenn die zukünftigen
Entscheidungen jedoch noch ungewiss sind, kann auch der Wert einer Stimme für
diese Entscheidungen von den Beteiligten noch gar nicht eingeschätzt werden,
sodass dann auch kein Stimmenmarkt existieren kann.
Wie aus diesen Überlegungen deutlich wird, werden
eigeninteressierte Individuen ihre Interessen im Mehrheitssystem nicht über
einen Stimmenmarkt verfolgen. Stattdessen werden sie sich in
Abstimmungsbündnissen bzw. Koalitionen zusammenschließen mit dem Ziel, durch
verbindliche Vereinbarungen über das gemeinsame Abstimmungsverhalten bestimmte
Alternativenbündel mehrheitlich durchzusetzen. {598}
Koalitionen bieten gegenüber dem individuellen
Stimmentausch eine Reihe von Vorteilen.
Zum einen sind die Verhandlungskosten
ganz erheblich niedriger, da mit einer Vereinbarung alle Koalitionsmitglieder
einbezogen werden können, die Vereinbarungen zwischen Koalitionen also 'en bloc'
stattfinden.
Zum andern wird durch die Zusammenfassung der Individuen in
Koalitionen mit kollektiven Präferenzen leichter überschaubar, welche
Alternativen überhaupt Aussichten auf eine Mehrheit haben und wieviele Stimmen
noch an der Mehrheit fehlen.
Koalitionen haben auch sehr viel eher als isolierte
Individuen die ausreichende Stimmkraft, um überhaupt erfolgversprechende
Anstrengungen zur Beeinflussung bestimmter Entscheidungen zu unternehmen.
Weiterhin können sich Koalitionen auch besser um die
kollektiv vorteilhaften Alternativen kümmern, da die Koalitionsvereinbarungen
ein Trittbrettfahrer-Verhalten ausschließen.
Koalitionen können sich außerdem
auch dort bilden, wo die zukünftig zu treffenden Entscheidungen noch gar nicht
ausformuliert feststehen. Kristallisationspunkte für Koalitionen in einer
solchen Situation können gemeinsame Absichtserklärungen und Programme sein, die
in relativ allgemeiner Weise die gemeinsamen Ziele festlegen, an denen sich dann
das spätere Abstimmungsverhalten der Koalitionspartner auszurichten hat. Dabei
besteht für alle Beteiligten in gleichem Maße die Ungewissheit darüber, ob und
wieweit eine Durchsetzung dieses Programms möglich sein wird. {599}
§ 128 Einzel-Punkt-Koalitionen und Mehr-Punkte-Koalitionen
Abstimmungskoalitionen lassen sich dadurch
charakterisieren, welche Individuen sie umfassen, über welche Entscheidungen
sich ihre Koalitionsvereinbarungen erstrecken und welche Alternativen der
Koalitionsvereinbarung zugrunde liegen. Einzel-Punkt-Koalitionen
werden durch Abstimmungsvereinbarungen gebildet, die nur eine einzelne
Entscheidung betreffen. Solche Einzel-Punkt-Koalitionen wurden in Kapitel 19
untersucht. Jedes Mitglied einer solchen Koalition ist nur verpflichtet, bei
einer bestimmten Entscheidung für eine bestimmte Alternative zu stimmen.
Um erfolgreich zu sein, müssen solche
Einzelpunkt-Koalitionen die erforderliche Mehrheit für ihre Alternative
erlangen. Reicht die Zahl der Koalitionsmitglieder hierzu noch nicht aus, so
muss
die Koalition versuchen, sich entsprechend zu vergrößern, indem sie Absprachen
mit weiteren Individuen eingeht. Damit diese jedoch für die
Koalitionsalternative stimmen - was sie als Nicht-Mitglieder der Koalition von
sich aus nicht tun würden - , muss ihnen die Einzelpunkt-Koalition ihrerseits in
einer andern Entscheidung entgegenkommen. Hieraus ergibt sich eine
Tendenz zur
Ausweitung von Einzel-Punkt-Koalitionen zu Mehr-Punkte-Koalitionen, die sich auf
mehrere Entscheidungen gleichzeitig erstrecken.
Nehmen wir z. B. an, eine Einzel-Punkt-Koalition K1 trifft
eine Vereinbarung mit einer anderen Koalition K2 mit dem Inhalt, dass die
Mitglieder von K1 bei der Entscheidung II für die Alternative u
stimmen, wenn {600} die Mitglieder von K2 bei der Entscheidung I für die
Alternative x stimmen.
Die Frage ist jedoch, ob alle Mitglieder von K1 mit der
Alternative u einverstanden sind. Die Koalition K1 hatte sich zugunsten der
Alternative x der Entscheidung I gebildet, und eine Interessenübereinstimmung
auf dem einen Gebiet kann ohne weiteres mit unterschiedlichen Interessen auf
einem andern Gebiet einhergehen. Auf ihren Vorteil bedachte Individuen werden
aber die Koalition K1 nach einer solchen Absprache verlassen, wenn das
Alternativenbündel "x mit u" ihren Interessen weniger entspricht als irgendein
anderes erfolgversprechendes Alternativenbündel zu den Entscheidungen I und II.
Einzel-Punkt-Koalitionen sind also relativ instabil, wenn
sie zur Erlangung der Mehrheit weitere Absprachen eingehen müssen. Wenn eine
Koalition im Zuge weiterer Absprachen also möglichst wenige Mitglieder verlieren
will, so muss sie Vereinbarungen in Bezug auf solche Alternativen suchen, die den
Interessen der eigenen Mitglieder möglichst gut entsprechen.
Je
unterschiedlicher die Interessen der Koalitionsmitglieder in Bezug auf
Entscheidungen außerhalb der ursprünglichen Koalitionsvereinbarung sind, umso
unbeweglicher und instabiler ist die Koalition und umso stärker sind die
Spannungen innerhalb der Koalition bei Versuchen zu einer Ausweitung der
Koalition. Je nachdem, welche zusätzlichen Vereinbarungen eingegangen werden,
werden andere Individuen die alte Koalition verlassen.[[13] Hier zeigt sich übrigens das Problem der Bildung eines
einheitlichen Willens zu weiteren Entscheidungen innerhalb einer Koalition, wenn
die Interessenlage ihrer Mitglieder nicht identisch ist. In gewisser Weise
wiederholt sich hier das Problem des Gesamtwillens auf partikularem Niveau.]
Schließen z. B. 2
Einzel-Punkt-Koalitionen eine Vereinbarung zur wechselseitigen
Unterstützung ihrer Alternativen ab, wenn die Interessenlage der Mitglieder in
Bezug auf die beiden Alternativen relativ gegensätzlich ist,
so kann der Fall
eintreten, dass diese Zwei-Punkte-Koalition schließlich über weniger Stimmkraft
verfügt als jede der beiden Koalitionen für sich genommen vor dieser
Vereinbarung besaß. Solche Bündnisse sind dann im Endeffekt schwächer als die
Teilkoalitionen, aus denen sie zusammengesetzt sind.
Am stabilsten und
beweglichsten in weiteren Koalitionsverhandlungen sind deshalb solche
Koalitionen, bei denen die wichtigsten Interessen ihrer Mitglieder bereits
positiv abgedeckt sind. Wenn sich eine Koalitionsvereinbarung bereits über viele
Entscheidungen hinweg mit den Präferenzen ihrer Mitglieder deckt, so kann jedes
Mitglied auch an einzelnen Punkten Koalitionsvereinbarungen akzeptieren, die
seinen Interessen weniger entsprechen. Gruppen von insgesamt gleichartig und
stark interessierten Individuen werden deshalb die Kristallisationskerne
darstellen, um die herum sich stabile größere Koalitionen aufbauen. [[14]
Welches in einer bestimmten Gesellschaft zu einem
bestimmten Zeitpunkt die wichtigsten
gemeinsamen Interessen sind, die damit koalitionsstiftend sind und auf deren
Grundlage sich z. B. politische Parteien bilden, ist hier nicht Gegenstand der
Untersuchung. Hier geht es nur um das allgemeine Modell des Mehrheitssystems,
das auf die verschiedensten inhaltlichen Interessenkonstellationen anwendbar
sein soll.]
Dabei ist
eine Vergrößerung der Mitgliederzahl einer Koalition in Richtung auf die
Mehrheit im allgemeinen auch mit einer Erweiterung des Bereichs der
Vereinbarungen verbunden, da eine Einigung am ehesten an solchen Punkten möglich
erscheint, wo sich keine der Seiten bisher schon festgelegt hat. {602}
§ 129 Rationale Koalitionsbildung bei Entscheidungsserien und das Mehrheitsalternativenbündel
Sofern es sich um ganze Entscheidungsserien handelt,
wird ein auf seinen Vorteil bedachtes Individuum nicht so sehr versuchen, bei den
einzelnen Entscheidungen ein für sich möglichst gutes Ergebnis durchzusetzen,
sondern es wird bemüht sein, in Bezug auf die Gesamtheit der Entscheidungen das bestmögliche Ergebnis durchzusetzen. Das Individuum steht
im Falle von Entscheidungsserien also nicht vor isolierten Entscheidungen zwischen Einzelalternativen,
sondern vor einer einzigen Entscheidung zwischen verschiedenen Alternativenbündeln.
Durch die Existenz von Koalitionsvereinbarungen zu mehreren
Entscheidungen gleichzeitig sind die verschiedenen Einzelentscheidungen nicht
mehr unabhängig voneinander, und es kommt für jedes Individuum darauf an, in
Kooperation mit andern eine Abstimmungsstrategie zu vereinbaren, die das
individuell beste Alternativenbündel durchsetzt. Dazu ist im Mehrheitssystem
jedoch immer eine Mehrheit der Individuen erforderlich, sodass entsprechende Mehrheits-Koalitionen gebildet werden müssen.
Wenn die Zahl der zu treffenden Entscheidungen und Zahl der
zugehörigen Alternativen gegeben ist, so lassen sich mit Hilfe der Kombinatorik
alle logisch möglichen Alternativenbündel bestimmen. Die Zahl der möglichen
Alternativenbündel beträgt bei k Entscheidungen mit jeweils n Einzelalternativen
nk. Die Zahl der möglichen Ergebnisse steigt also mit wachsender Zahl der
Alternativen exponential an. Bei jeweils 3 Einzelalternativen pro Entscheidung
beträgt die {603} Zahl möglicher Alternativenbündel
bei 1 Entscheidung 31
=
3,
bei 2 Entscheidungen 32 = 9,
bei 3 Entscheidungen 33 = 27 und
bei 4
Entscheidungen bereits 34 = 81 Alternativenbündel.
Aus diesem Grund müssen sich
die folgenden Überlegungen auf relativ einfache Beispiele konzentrieren.
Man kann nun die Interessenlage der Individuen in Bezug auf
diese Alternativenbündel ebenso wie bei den Einzelalternativen durch eine
Präferenzordnung wiedergeben. Dies soll an einem Beispiel mit 5
Individuen A bis E und 3 Einzelentscheidungen mit jeweils 2 Einzelalternativen
veranschaulicht werden. [[15] Die Präferenzen der Individuen in Bezug auf die
Einzelalternativen spielen hier keine Rolle und werden deshalb nicht
wiedergegeben.] Es ergeben sich dann 32 = 9 Alternativenbündel als
logisch mögliche Ergebnisse dieser Abstimmungsserie. Diese Alternativenbündel
sollen mit den Ziffern 1 bis 9 bezeichnet werden. Die Präferenzordnungen der
Individuen in Bezug auf diese Alternativenbündel seien wie folgt:
Präferenzordnungen (in Bezug auf Alternativenbündel 1 bis 9)
| A | B | C | D | E | |
| 1. | 1 | 8 | 2 | 5 | 4 |
| 2. | 2 | 9 | 3 | 4 | 5 |
| 3. | 4 | 2 | 8 | 2 | 1 |
| 4. | 7 | 3 | 9 | 1 | 2 |
| 5. | 3 | 5 | 1 | 6 | 6 |
| 6. | 5 | 7 | 5 | 8 | 7 |
| 7. | 6 | 1 | 7 | 3 | 3 |
| 8. | 8 | 6 | 6 | 7 | 8 |
| 9. | 9 | 4 | 4 | 9 | 9 |
Abb.: 21.9
{604} Jedes auf seinen Vorteil bedachte Individuum wird nun
versuchen, auf der Grundlage der von ihm bevorzugten Alternativenbündel Mehrheitskoalitionen zu bilden.
[[16] Bei den folgenden Überlegungen wird davon ausgegangen,
dass sich Globalkoalitionen bilden, d.h. solche Koalitionen, deren
Abstimmungsvereinbarungen sich über sämtliche Entscheidungen erstrecken und
damit ein vollständiges Alternativenbündel umfassen. Damit ist ausgeschlossen,
dass sich wechselnde Mehrheiten bei den Einzelentscheidungen bilden. Es bliebe zu
untersuchen, ob solche Globalkoalitionen bei vollkommen rationaler
Koalitionsbildung in jedem Fall zustande kommen müssen.]
Ergibt sich für das von ihm
bevorzugte Alternativenbündel keine Mehrheit, so wird das Individuum versuchen, eine
Mehrheits-Koalition auf der Basis des nächstbesten Alternativenbündels zu bilden
usw. Damit stellt sich das Problem, für welches der Alternativenbündel sich eine
erfolgreiche Mehrheits-Koalition bildet analog zur Mehrheitsbildung bei
Einzelalternativen. Der Unterschied ist nur, dass diesmal über globale
Alternativenbündel in mehreren Einzelabstimmungen entschieden wird.
Da es sich in diesem Fall um ein individuell
gleichgewichtiges Abstimmungsverfahren handelt, denn alle Individuen nehmen mit
je einer Stimme an allen Einzelabstimmungen teil, lässt sich auch hier das oben
formulierte Äquivalenz-Theorem anwenden, das besagt, dass sich bei rationaler
Koalitionsbildung aller Individuen eine vorhandene Mehrheitsalternative
durchsetzt.
In unserm Beispiel existiert eine solche Mehrheitsalternative in
Gestalt des Alternativenbündels 2, wie die folgende Wahlmatrix zeigt:{605}
Wahlmatrix zu Abb.21.9
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
- |
2:3 |
3:2 |
3:2 |
2:3 |
5:0 |
4:1 |
3:2 |
3:2 |
|
2 |
3:2 |
- |
5:0 |
3:2 |
3:2 |
5:0 |
5:0 |
4:1 |
4:1 |
|
3 |
2:3 |
0:5 |
- |
2:3 |
3:2 |
3:2 |
4:1 |
3:2 |
4:1 |
|
4 |
2:3 |
2:3 |
3:2 |
- |
2:3 |
3:2 |
3:2 |
3:2 |
3:2 |
|
5 |
3:2 |
2:3 |
2:3 |
3:2 |
- |
5:0 |
4:1 |
3:2 |
3:2 |
|
6 |
0:5 |
0:5 |
2:3 |
2:3 |
0:5 |
- |
2:3 |
3:2 |
3:2 |
|
7 |
1:4 |
0:5 |
1:4 |
2:3 |
1:4 |
3:2 |
- |
2:3 |
3:2 |
|
8 |
2:3 |
1:4 |
2:3 |
2:3 |
2:3 |
2:3 |
3:2 |
- |
5:0 |
|
9 |
2:3 |
1:4 |
1:4 |
2:3 |
2:3 |
2:3 |
2:3 |
0:5 |
- |
Abb.: 21.10
Wie man sieht, ist das Alternativenbündel 2 im Paarvergleich
allen andern Alternativenbündeln überlegen. Es findet sich gegenüber jedem
andern Alternativenbündel also immer mindestens eine Mehrheit von 3 der 5
Individuen, für die das Alternativenbündel 2 besser ist. Bündel 2 kann deshalb
als Mehrheitsalternativenbündel bezeichnet werden. Entsprechend dem
Äquivalenz-Theorem wird sich Bündel 2 damit bei vollkommen rationaler
Koalitionsbildung im Rahmen eines individuell gleichgewichtigen Abstimmungsverfahrens,
z. B. nach der relativen Mehrheitsregel, durchsetzen.
Wenn z. B. die Individuen A, D und E versuchen würden, eine
Mehrheitskoalition auf der Basis des Bündels 1 zu bilden, so könnten B und C das
Individuum D davon überzeugen, dass eine Koalition zwischen ihnen auf
der Basis 2 für D besser wäre, denn das Alternativenbündel 2 steht in der
Präferenzordnung von D vor dem Bündel 1. Gäbe es z. B. eine Koalition zwischen B,
D und E auf der Basis 5, so könnten A und C Individuum B davon überzeugen, dass
eine Koalition zwischen ihnen auf der Basis 2 für B vorteilhafter wäre.
Ist
jedoch einmal eine Mehrheits-Koalition auf der {606} Basis des Mehrheitsalternativenbündels 2
etabliert, so gibt es kein anderes Alternativenbündel, auf dessen Grundlage sich
eine andere Mehrheitskoalition bilden könnte. Auch bei
Entscheidungs-Serien bildet also die Mehrheitsalternative den Gleichgewichtspunkt.
Dabei ist noch anzumerken, dass auch hier mit Hilfe einer solchen Analyse zwar
der Inhalt der schließlich siegreichen Koalitionsvereinbarung bestimmt werden
kann, jedoch nicht ihre personelle Zusammensetzung.
§ 130 Zur Verhandlungsmacht bei Koalitionsbildungen
Wie in den vorangegangenen Kapiteln dargelegt wurde, kommt
es im Mehrheitssystem bei eigeninteressiertem Verhalten der Individuen zu
Koalitionsvereinbarungen zwischen den Individuen bzw. Gruppen. Damit stellt sich die Frage nach der Verhandlungsmacht, die die
verschiedenen Verhandlungspartner besitzen. [[17] Vgl. hierzu BUCHANAN/TULLOCK 1969, S.68f. Übrigens ist
für sie die monopolistische Verhandlungsmacht jedes Individuums und die daraus
resultierenden Verhandlungskosten der entscheidende Grund für ein Abgehen von
der Einstimmigkeits-Regel und die Akzeptierung der Mehrheitsregel.]
Im Mehrheitssystem wird die
Verhandlungsmacht eines Individuums oder einer Gruppe immer dadurch begrenzt,
dass noch weitere potentielle Koalitionspartner existieren, mit denen ebenfalls
eine Mehrheits-Koalition gebildet werden kann. Es besteht hier also immer eine
Konkurrenz zwischen den potentiellen Koalitionspartnern, denn kein Individuum
und keine Gruppe ist hier als Koalitionspartner unersetzlich.
Dies ist in Einstimmigkeits-Systemen
anders, da dort jedes Individuum mit seiner Zustimmung für die kollektive
Entscheidung unersetzlich ist und folglich eine monopolistische {607}Verhandlungsmacht besitzt.
Je niedriger der zur
Durchsetzung einer Alternative erforderliche Stimmenanteil ist, umso
geringer ist die Verhandlungsmacht des einzelnen Individuums, da die Zahl der
Individuen, die es ersetzen können, steigt.
Ein Individuum oder eine Gruppe wird dabei die
Koalitionsverhandlungen dann abbrechen, wenn die Forderungen des
Verhandlungspartners zu einem Alternativenbündel führen würden, das schlechter
ist als eine mögliche Koalitionsvereinbarung im Rahmen einer anderen
Mehrheits-Koalition. Daraus wird deutlich, dass die Verhandlungsmacht einer
Gruppe im Rahmen des Mehrheitssystems weniger von ihrer zahlenmäßigen
Stärke abhängt als von der vorhandenen Gesamtkonstellation und der
Beschaffenheit des Mehrheitsalternativenbündels.
So kann u. U. eine relativ kleine Gruppe, die in ihrer
Interessenlage eine Mittelstellung zwischen zwei großen Gruppen einnimmt und
deren Spitzen-Alternativenbündel zugleich das Mehrheitsalternativenbündel ist,
als "Zünglein an der Waage" ihren großen Koalitionspartner zu relativ
weitgehenden Konzessionen zwingen. Dies soll an einem einfachen
3-Gruppen-Beispiel verdeutlicht werden.
Angenommen Gruppe A umfasst 42% der
Individuen, Gruppe B 10% und Gruppe C 48%. Die Interessenlage der beiden großen
Gruppen A und C in Bezug auf die 3 Alternativenbündel 1, 2 und 3 sei genau entgegengesetzt, d.h. dass ihre Präferenzordnungen
genau die umgekehrte Reihenfolge der {608} Alternativen aufweisen. Die kleine Gruppe C soll in ihrer
Interessenlage dabei eine Mittelstellung einnehmen, sie bevorzugt jedoch das
Spitzen-Alternativenbündel bzw. das "Programm" der Gruppe A (also 1) leicht vor dem der
Gruppe C (also 3). Dabei sind die intrasubjektiven Präferenzintensitäten wiederum durch
den Abstand zwischen den Alternativenbündeln ausgedrückt:
Präferenzordnungen (mit Intensitäten)
| A (42%) | B (10%) | C (48%) |
| 1 | 2 | 3 |
| - | - | - |
| 2 | - | 2 |
| - | 1 | - |
| 3 | 3 | 1 |
Abb.: 21.11
In einer solchen Interessenkonstellation kommt eigentlich
nur eine Koalition zwischen B und A oder B und C in Frage, da B eine Mittelstellung einnimmt.
[[18] Es sei denn, B hätte sich durch überzogene Forderungen
bei A und C selber "austaktiert".]
Wenn einmal annimmt, dass diese 3 "Programme" nicht die
einzigen Alternativen darstellen, sondern dass es noch eine Reihe von
Zwischenformen gibt, die ebenfalls mögliche Ergebnisse darstellen, so reicht der
Konzessionsbereich der Gruppe A gegenüber der Gruppe B bis an das
Alternativenbündel 2, dem Programm der Gruppe B.
Alle Alternativenbündel, die nutzenmäßig zwischen den Bündeln 1 und 2 rangieren, sind für die Gruppe A immer
noch besser als der Abbruch der Koalitionsverhandlungen mit B, denn das würde
eine Koalition zwischen den Gruppen B und C bedeuten auf der Grundlage eines
Alternativenbündels, das für A wahrscheinlich zwischen den Bündeln 2 und 3
liegen würde, also schlechter wäre als Bündel 2. Aus diesem {609} Grund ist die Verhandlungsmacht von B gegenüber A relativ
groß, denn B kann immer mit dem Abbruch der Verhandlungen drohen, während B für
A als Koalitionspartner praktisch unersetzlich ist, da eine Koalition mit C
nicht in Frage kommt.
Für die Gruppe B wäre deshalb bei einer solchen
Interessenkonstellation eine Koalitionsvereinbarung mit A auf der Grundlage
eines Alternativenbündels 2' möglich, das nur eine geringfügige Modifikation des
Bündels 2 entsprechend den Interessen der Gruppe A darstellt.
Der größere
Koalitionspartner ist bei einer solchen Interessenkonstellation im Mehrheitssystem also zu weitergehenden Zugeständnissen gezwungen als der
kleinere Koalitionspartner. Dabei ist die Feststellung von Bedeutung, dass sich
die relativ starke Verhandlungsposition der Gruppe B allein aus ihrer interessemäßigen Mittelstellung zwischen den beiden andern Gruppen ergibt.
Selbst wenn die zahlenmäßigen Stärkeverhältnisse zwischen den Gruppen A und B
umgekehrt wären und A einen Anteil von 10% und B einen Anteil von 42% der
Individuen besitzen würde, könnte die Gruppe B für sich keine vorteilhaftere
Koalitionsvereinbarung abschließen.
Übrigens kann ein relativ weites Entgegenkommen der Gruppe
A gegenüber den Zielen der Gruppe B auch noch unter einem anderen Gesichtspunkt
für die Gruppe A geboten sein. Da Koalitionen im Mehrheitssystem Zweckbündnisse
darstellen, die von den Mitgliedern verlassen werden können, wenn sie
individuell nachteilig geworden sind, besteht bei einem größeren Entgegenkommen
der Mittelgruppe B gegenüber der Gruppe A die Gefahr, dass einige Mitglieder der
Gruppe B, die {610} mit dieser Entscheidung ihrer Koalitionsführung nicht
einverstanden sind, ihre bisherige Koalition verlassen und zur Gruppe C
überwechseln, sodass diese Gruppe jetzt die absolute Mehrheit bekommen würde und
das Alternativenbündel 3 durchsetzen könnte. Dies wäre für die Gruppe A dann das
schlechteste aller möglichen Ergebnisse. Auch aus diesem Grund wird die Gruppe A
also bei den Koalitionsverhandlungen mit B relativ entgegenkommend sein.
Die besondere Verhandlungsmacht einer kleinen Mittelgruppe
gegenüber allen potentiellen Koalitionspartnern hängt damit zusammen, dass sich
das interessemäßig "mittlere" Individuum in dieser Gruppe befindet und
dass das
Programm der Mittelgruppe gewissermaßen die Mehrheitsalternative darstellt. [[19]
Zum Zusammenhang zwischen medianer Spitzenalternative
und Mehrheitsalternative s.o. § 111.]
Um dies zu veranschaulichen, soll von der vereinfachenden Annahme ausgegangen werden, dass alle drei Gruppen in sich interessemäßig homogen sind, sodass ihre Mitglieder jeweils identische Präferenzordnungen aufweisen. In diesem Fall decken sich die Präferenzen der Gruppen völlig mit den Interessen jedes einzelnen Gruppenmitglieds. Bei einem Paarvergleich der Bündel 1, 2 und 3 bezogen auf 100 Individuen ergäbe sich dann folgende Wahlmatrix:
Wahlmatrix zu
Abb.21.11
| 1 | 2 | 3 | |
| 1 | - | 42:58 | 52:48 |
| 2 | 58:42 | - | 52:46 |
| 3 | 48:52 | 48:52 | - |
Abb.: 21.12
{611} Wie man sieht, bildet die Spitzenalternative der kleinen
Mittelgruppe B, das Bündel 2 zugleich die Mehrheitsalternative, wenn man von in sich
homogenen Gruppen ausgeht. Aus diesem Grunde wäre es auch entgegen der inneren
Logik des Mehrheitssystems, wenn man kritisieren würde, dass die kollektiven
Entscheidungen in so starkem Maße nach dem Willen einer relativ kleinen Gruppe
verlaufen. Entscheidend ist hier nicht die zahlenmäßige Stärke sondern die
Tatsache, dass sich die Präferenzen dieser Gruppe mit der Mehrheitsalternative
decken.
Die normative Rechtfertigung des Mehrheitssystems liegt darin, dass es
zur Durchsetzung einer vorhandenen Mehrheitsalternative führt, die unter
bestimmten Voraussetzungen als eine Annäherung an das Gesamtinteresse
verstanden werden kann. [[20] Zum Verhältnis zwischen der Mehrheitsalternative und
der Alternative des maximalen Gesamtnutzens s.u. § 139.] {612}
22. Kapitel
Die normative Beurteilung des Mehrheitssystems
§ 131 Mehrheitsprinzip und Gleichgewichtung der
individuellen Präferenzordnungen
Im Mehrheitssystem werden die individuellen Präferenzordnungen zu einer kollektiven Entscheidung zusammengefasst. Dabei spielt es keine Rolle, von welchem Individuum welche Präferenzordnung stammt. Bei Anwendung der relativen Mehrheitsregel ist es z. B. ohne Einfluss auf das Ergebnis der Abstimmung, ob eine bestimmte Stimme von Individuum A oder B stammt: jede Stimme zählt in gleicher Weise. Dies ermöglicht auch eine geheime Stimmabgabe, was unter dem Gesichtspunkt einer sanktionsfreien Äußerung der individuellen Interessen von Bedeutung sein kann. Die relative Mehrheitsregel besitzt also die Eigenschaft der Anonymität, die erfordert, dass bei einer gegebenen Menge von Präferenzen durch deren Vertauschung zwischen den Individuen die kollektive Präferenz nicht verändert werden darf. [[1] Zur Bedingung der Anonymität vgl. MAY 1952 sowie SEN 1970, S.68.]
Die Eigenschaft der Anonymität gilt dabei nicht nur für die
relative Mehrheitsregel sondern für alle individuell gleichgewichtigen
Abstimmungsverfahren unter der Bedingung rationaler Koalitionsbildung. All diese
Verfahren führen unter diesen Bedingungen zur Durchsetzung der {613} Mehrheitsalternative.
Zu deren Feststellung z. B. durch
eine Wahlmatrix muss man jedoch nicht wissen, wer welche Präferenzordnungen
besitzt, denn in der Wahlmatrix tauchen überhaupt keine Individuennamen auf.
Die Eigenschaft der Anonymität für das Mehrheitssystem
ergibt sich also aus der grundlegenderen Eigenschaft, dass im Mehrheitssystem
die allerdings nur ordinal bestimmten individuellen Nutzen gleiches Gewicht erhalten. Dies erfordert, dass alle Individuen an allen Abstimmungen
teilnehmen und dass sie jeweils die gleiche Stimmen- bzw. Punktzahl zu vergeben
haben.
Diese Beziehung zwischen Mehrheitsprinzip und der Gleichheitsforderung
macht DOWNS deutlich. "Die grundlegende Prämisse hinter der einfachen
Mehrheitsregel ist, dass jedem Wähler das gleiche Gewicht zukommen soll wie
jedem andern Wähler. Danach ist es im Falle der Uneinigkeit besser, wenn mehr
Wähler weniger Wählern vorschreiben, was zu tun ist, als umgekehrt. Jede Regel,
die mehr als eine einfache Mehrheit für die Zulassung einer Handlung fordert,
erlaubt einer Minderheit, die Aktion einer Mehrheit zu verhindern, wodurch der
Stimme jedes Mitglieds der Minderheit ein größeres Gewicht gegeben wird als der
Stimme jedes Mitglieds der Mehrheit." [[2] DOWNS 1961, S.192. In gleicher Weise argumentieren auch
DAHL/LINDBLOM 1963, S.44.]
In diesem egalitären Aspekt des Mehrheitsprinzips liegt ein
wichtiger Unterschied zum Eigentum-Vertrags-System, das mit keiner bestimmten
Gewichtung der individuellen Interessen verbunden ist. {614}
Je nach der Verteilung des Eigentums auf die Individuen -
und das heißt vor allem: je nach der Verteilung des Eigentums an
Produktionsfaktoren - bekommen die Präferenzen der Individuen im
Eigentum-Vertrags-System ihr Gewicht. Je unterschiedlicher das Produktivvermögen
auf die Individuen einer Gesellschaft verteilt ist, umso unterschiedlicher
werden ihre Interessen bei der kollektiven Entscheidung berücksichtigt.
Wenn man
z. B. die Verteilung von Gütern über den Markt als ein Wahlverfahren
interpretiert, so hieße das, dass jedem Individuum entsprechend seinem Einkommen
eine unterschiedliche Zahl von Stimmen bzw. Punkten zugeteilt wird. [[3] Vgl. hierzu BERNHOLZ 1972, S.105f.]
Unter dem Gesichtspunkt einer solidarischen
Berücksichtigung der individuellen Interessen erscheint das Mehrheitsprinzip
also geeigneter als das Eigentum-Vertrags-System, das immanente Tendenzen zu
einer immer ungleicheren Verteilung des Eigentums auf die Individuen enthält. [[4]
Zu kumulativen Tendenzen des Eigentums s.o. § 85.]
Allerdings erfolgt im Mehrheitssystem immer nur eine Gleichgewichtung der ordinal ermittelten individuellen Nutzen,
da nur die individuellen
Präferenzordnungen berücksichtigt werden. Es kann folglich im Mehrheitssystem
keine interpersonal vergleichbare Abwägung der Dringlichkeit von Interessen
verschiedener Individuen vorgenommen werden. [[5] Zur Nicht-Berücksichtigung von Präferenzintensitäten s.u.
§ 138.] {615}
§ 132 Weitere Eigenschaften des Mehrheitsprinzips
Im Rahmen von Untersuchungen über die Logik kollektiver
Entscheidungen wurden weitere Eigenschaften des Mehrheitsprinzips bestimmt,
wobei darunter immer der paarweise Vergleich gemäß CONDORCET verstanden wird,
der zur Auswahl der Mehrheitsalternative führt. Da jedoch im Falle rationaler
Koalitionsbildung alle individuell gleichgewichtigen Abstimmungsverfahren
ebenfalls zur Auswahl der Mehrheitsalternative führen, können diese Ergebnisse
auf diese Verfahren übertragen werden. [[6] Zum Folgenden s. SEN 1970,
S.116ff.]
Offensichtlich ist, dass die Mehrheitsregel nicht
diktatorisch ist. Es gibt also kein Individuum, dessen Wille für die kollektive Entscheidung
allein maßgebend ist unabhängig davon, was die übrigen Individuen wollen. [[7]
Zur Bedingung der Nicht-Diktatur s. ARROW 1963, S.30.]
Außerdem beinhaltet die Mehrheitsregel eine positive Entsprechung (positive responsiveness) zwischen den
individuellen Präferenzen und der kollektiven Präferenz.
Für eine
Entscheidungsregel, die dieser Bedingung genügen soll, muss gelten: "Wenn x in
bestimmten Situationen als kollektiv ebenso gut angesehen wird wie y und x dann
in der Präferenz irgendeines Individuums gegenüber y steigt, ohne in der
Präferenz von irgendjemand zu fallen, so muss x daraufhin als eindeutig besser
als y angesehen werden." [[8] SEN 1970, S.68.]
Dass diese Bedingung durch das Mehrheitsprinzip {616} erfüllt wird, lässt sich ebenfalls leicht zeigen. Wenn
die Alternativen x und y zuerst im Paarvergleich Stimmengleichheit hatten und
deshalb als kollektiv gleich gut angesehen wurden, so muss jede individuelle
Änderung der Präferenz zwischen x und y zugunsten von x zur Stimmenmehrheit von
x führen, die damit zur kollektiv besseren Alternative wird.
Weiterhin ist das Mehrheitsprinzip neutral gegenüber den
zur Entscheidung anstehenden Alternativen und bevorzugt nicht systematisch
bestimmte Alternativen. "Neutralität verlangt: Wenn im Fall 1 zwei Alternativen
x und y in den Präferenzen jedes Individuums genau die gleiche Beziehung
zueinander haben wie z und w im Fall 2, dann muss die soziale Präferenz zwischen
x und y im Fall 1 genau die gleiche sein wie die soziale Präferenz zwischen z
und w im Fall 2." [[9] SEN 1970, S.72.]
Auch die Neutralitäts-Bedingung wird vom Mehrheitsprinzip
offensichtlich erfüllt, denn für den Paarvergleich spielen Art oder Bezeichnung
der Alternativen keine Rolle, es kommt allein auf Rangordnung der beiden
Alternativen in den individuellen Präferenzen an.
Auch die Bedingung des unbeschränkten Bereichs
(unrestricted domain) der Präferenzen wird vom Mehrheitsprinzip erfüllt. Diese
Bedingung besagt, dass alle logisch möglichen individuellen Präferenzrangfolgen
der Alternativen zugelassen sein müssen. [[10] Siehe dazu ARROW 1963, 3.24 und SEN 1970, S.37.]
{617}
Zuletzt sei noch die Bedingung der Unabhängigkeit von
irrelevanten Alternativen erwähnt, die das Mehrheitsprinzip ebenfalls erfüllt.
Diese Bedingung verlangt, dass die kollektive Entscheidung zwischen
verschiedenen Alternativen allein auf den individuellen Rangordnungen derjenigen Alternativen beruhen muss, die
tatsächlich zur Entscheidung stehen. "Angenommen es geht um die Wahl zwischen x
und y und die individuellen Rangordnungen von x und y bleiben dieselben, nur die
Rangordnung von x gegenüber irgendeiner anderen Alternative z verändert sich
oder die Rangordnung von z gegenüber einer weiteren Alternative w wechselt. In
diesem Fall ist zu fordern, dass die soziale Wahl zwischen x und y weiterhin
unverändert bleiben soll." [[11] SEN 1970, S.37. Siehe zu diesen Bedingungen auch die
Diskussion des ARROW-Theorems oben § 37/3.]
MAY hat nun nachgewiesen, dass die Mehrheitsregel die
einzige kollektive Entscheidungs-Regel ist, die die genannten fünf Bedingungen
erfüllt (Unbeschränkter Bereich der individuellen Präferenzen, Unabhängigkeit
der kollektiven Entscheidung von irrelevanten Alternativen, Anonymität in Bezug
auf die Individuen, Neutralität gegenüber den Alternativen, Positive
Entsprechung individueller und kollektiver Präferenzen) und die außerdem noch
insofern entscheidungsfähig ist, als sie für jedes beliebige Alternativenpaar x
und y angeben kann, ob x mindestens ebenso gut ist wie y oder y ebenso gut ist
wie x. [[12] Siehe MAY 1952 sowie den Beweis bei SEN 1970, S. 71ff.
Zur genauen Definition des Begriffs "entscheidungsfähige kollektive Entscheidungs-Regel" (decisive collective choice rule) s. SEN 1970, S.23 u. 28.]
Allerdings muss sich bei mehr als zwei Alternativen mit Hilfe der
Mehrheitsregel nicht immer eine eindeutige Rangordnung der Alternativen ergeben
aufgrund zirkulärer Mehrheiten. [[13] Siehe dazu unten § 136.1]
§ 133 Mehrheitsprinzip und kollektive Betroffenheit von Entscheidungen
Als ein problematischer Punkt des Eigentum-Vertrags-Systems
war oben die häufig mangelnde Abgrenzbarkeit der individuellen
Verfügungsbereiche diskutiert worden, die zu nicht vertraglich geregelten
Einwirkungen zwischen den Eigentumssphären führt, sei es in Form der sogenannten
kollektiven Güter oder aber der externen Effekte. [[14] Siehe dazu oben Kap.14.]
Solche Probleme ergeben sich
bei Anwendung des Mehrheitsprinzips nicht, da hier die Individuen nicht nur für
einen jeweils separaten Bereich zuständig sind, sondern alle Individuen ihren
Interessen zu allen Aspekten der zur Entscheidung anstehenden Alternativen
Ausdruck geben können. Es kann also bei Anwendung des Mehrheitsprinzips nicht
der Fall sein, dass ein Individuum negativ oder positiv von bestimmten
Entscheidungen betroffen wird, ohne dass nicht auch sein Interesse - wenn auch
als eines unter vielen - dabei berücksichtigt wurde. [[15] Zur Modifizierung der reinen Mehrheitsregel durch
abgegrenzte kollektive oder individuelle Verfügungsbereiche s.u. § 142. In
diesem Fall stellt sich auch für das Mehrheitsprinzip das Problem externer
Effekte.]
Ganz allgemein lässt
sich deshalb vorläufig festhalten, dass unter dem Gesichtspunkt der {619}Berücksichtigung aller betroffenen Interessen
das
Mehrheitsprinzip dann dem Eigentum-Vertrags-System vorzuziehen ist, wenn sich
Auswirkungen von Entscheidungen nicht auf individuelle Verfügungsbereiche
beschränken lassen.
Allerdings können Eigentum-Vertrags-System und
Mehrheitssystem u. U. auch miteinander kombiniert werden, um einmal die eher
individuellen und das andere mal die eher kollektiven Effekte zu regeln. So kann
man z. B. das Eigentumsrecht an bestimmten Gütern durch mehrheitlich beschlossene
Normen auf bestimmte Verwendungsarten einschränken. So mag etwa das
Eigentumsrecht an Motorrädern erhalten bleiben, aber es kann ihren Eigentümern
verboten sein, damit eine bestimmte Lautstärke zu überschreiten. Oder es mag das
Eigentumsrecht an Geldvermögen erhalten bleiben, aber dies Vermögen darf nicht
als privates Kapital zur Anstellung von Lohnarbeitern verwandt werden.
§ 134 Der Informations- und Entscheidungsaufwand im Mehrheitssystem
Die Tatsache, dass im Mehrheitssystem nicht nur auf die
eigene Verfügungssphäre beschränkte Interessen berücksichtigt werden, hat jedoch
auch verschiedene Nachteile unter dem Gesichtspunkt einer Maximierung des
Gesamtnutzens. Neben der Nicht-Berücksichtigung der unterschiedlichen
Betroffenheit der Individuen, auf die unten noch näher eingegangen wird,
treten
durch ein solches Mitentscheidungsrecht aller Individuen bei allen
Entscheidungen erhebliche Kosten der Informationsbeschaffung und der
Entscheidungsdurchführung auf. {620}
Jedes Individuum muss jetzt bei jeder Entscheidung jede
Alternative in all ihren Aspekten kennen und bewerten, um eine qualifizierte
Präferenzordnung dieser Alternativen aufstellen zu können. Außerdem müssen
sämtliche individuellen Präferenzen dann erfasst und über das
Abstimmungsverfahren und ihre teilweise komplizierten Koalitionsbildungen
aggregiert werden.
Dabei wird klar, dass unter dem Gesichtspunkt des
Gesamtnutzens der immense Entscheidungsaufwand die Vorteile durch die Wahl der
Mehrheitsalternative wahrscheinlich in vielen Fällen zunichte machen wird.
Selbst wenn Verfahren zur Senkung des Entscheidungsaufwands benutzt werden, wie
die oben diskutierten Beratungs- und Vertretungsverfahren oder die Aufstellung
genereller Normen, so bleibt doch der Entscheidungsaufwand gewaltig: Es müssen
ständig auf der Ebene des Gesamtkollektivs alle möglichen Entscheidungen
getroffen werden, um mögliche Konflikte zu regeln, bis hin zu kleinsten Details individuellen Verhaltens.
Aus diesem Grund liegt auch für das Mehrheitsprinzip eine
Modifizierung durch die Bildung individueller und kollektiver Zuständigkeitsbereiche nahe.
[[16] Zur Bildung kollektiver und individueller
Verfügungsbereiche im Rahmen des Mehrheitssystems siehe unten § 142.] Dadurch dass die Individuen dann nicht mehr mit
allen Entscheidungen befasst sind, sondern nur noch mit denjenigen, für die ihr
Teilkollektiv zuständig ist, sinkt der Entscheidungsaufwand erheblich. {621}
§ 135 Mehrheitsprinzip und Status-quo-Klausel
Verschiedene der oben besprochenen Abstimmungsverfahren
führen nicht notwendig zu einer eindeutigen kollektiven Entscheidung. So kann
man etwa bei der absoluten Mehrheitsregel durch die Einfügung einer
Status-quo-Klausel sicherstellen, dass es auch dann zu einer definitiven
Entscheidung kommt, wenn keine der zur Entscheidung stehenden Alternativen die
absolute Mehrheit der Stimmen erhält.
Durch den Zusatz einer Status-quo-Klausel werden diejenigen
Individuen zu Abstimmungskoalitionen motiviert, die Gewinnaussichten für eine
Alternative sehen, der sie gegenüber dem Status quo den Vorzug geben. Insofern
kann die Einführung der Status-quo Klausel also bewirken, dass jetzt eine
Alternative die erforderliche Mehrheit bekommt, die sie ohne
Status-quo-Klausel nicht bekommen hätte. Die Einführung einer Status-quo-Klausel
ruft also selber Kräfte auf den Plan, die an einer Vermeidung der
Status-quo-Lösung interessiert sind. [[17] Eine Illustration hierfür gibt das Beispiel in Kap. 20.]
Im Prinzip gilt auch für das Mehrheitssystem, dass durch
die Einführung einer Status-quo-Klausel ein konservativer Aspekt in das
Entscheidungsverfahren kommt, denn eine bestimmte Alternative - die Beibehaltung
des bestehenden Zustandes - wird dadurch gegenüber anderen Alternativen
bevorzugt behandelt. [[18] Vgl. z. B. die obige Kritik an der Verbindung von
Einstimmigkeits-Regeln und Status-quo-Klauseln in § 71.] {622}
Die Status-quo-Klausel wirkt sich in Verbindung mit der
absoluten Mehrheitsregel jedoch lange nicht so scharf aus wie in Verbindung mit
Einstimmigkeits-Regeln, wo bereits das Veto eines einzigen Individuums eine
Veränderung des Status quo unmöglich macht. Bei Anwendung der absoluten
Mehrheitsregel muss eine den Status quo verändernde Alternative nur von mehr als
50% der Individuen gegenüber dem Status quo vorgezogen werden, um sich
durchzusetzen, und nicht von 100%.
Im absoluten Mehrheitssystem mit rationaler
Koalitionsbildung gibt die Status-quo-Klausel genaugenommen nur in dem einzigen
Fall den Ausschlag, wo genau 50% der Individuen den Status quo gegenüber einer
Alternative x befürworten und 50% die Alternative x gegenüber dem Status quo. In
allen andern Fällen bekommen bei rationaler Koalitionsbildung entweder der Status
quo oder die konkurrierende Alternative eine absolute Mehrheit, sodass die
Status-quo-Klausel keine Rolle spielt.
§ 136 Zyklische Mehrheiten und das Problem der Instabilität im Mehrheitssystem
In den vorangegangenen Untersuchungen war immer
vorausgesetzt worden, dass eine Mehrheitsalternative existiert. Unter dieser
Bedingung war z. B. auch das Äquivalenz-Theorem formuliert worden. Wie jedoch
bereits mehrfach angesprochen und wie ARROW in seinem "Allgemeinen
Unmöglichkeits-Theorem" bewiesen hat, kann das Mehrheitsprinzip in der Form
des Paarvergleichs zu zyklischen Mehrheiten führen, indem eine Alternative x
gegenüber der Alternative y von einer Mehrheit vorgezogen wird, desgleichen y
gegenüber z und zugleich wiederum z gegenüber x. Wenn {623} in derartige Zirkeln auch die kollektiv besten Alternativen
einbezogen sind, sodass keine Alternative in allen Paarvergleichen überlegen ist,
so gibt es überhaupt keine Mehrheitsalternative.
Ein Beispiel für das Fehlen einer Mehrheitsalternative
geben folgende zirkuläre Präferenzordnungen:
Präferenzordnungen
(zirkulär)
| A | B | C |
| x | y | z |
| y | z | x |
| z | x | y |
Abb. 22.1
Die zugehörige Wahlmatrix sieht folgendermaßen aus:
Wahlmatrix zu Abb. 22.1
| x | y | z | |
| x | - | 2:1 | 1:2 |
| y | 1:2 | - | 2:1 |
| z | 2:1 | 1:2 | - |
Abb. 22.2
Wie man sieht, schlägt bei dieser Interessenkonstellation
im Paarvergleich jede Alternative einmal eine andere Alternative und wird einmal
selber geschlagen. Es gibt Mehrheiten für x gegenüber y, für y gegenüber z, aber
auch für z gegenüber x.
Dies bereits lange bekannte Abstimmungsparadox führt zum Fehlen einer Mehrheitsalternative, sofern
die zirkulären Mehrheiten an
der Spitze der kollektiven Präferenzordnung auftreten, wie in diesem Fall. Wenn
dagegen eine Mehrheitsalternative existiert, die in allen Paarvergleichen eine
Mehrheit erhält, und wenn nur bei den nachgeordneten Alternativen solche zyklischen
Mehrheiten auftreten, so ist das für die kollektive Entscheidung
unproblematisch, da es ja nur um die {624} Bestimmung der kollektiv besten Alternative geht.
Um die praktische Bedeutsamkeit dieses Problems zu
beurteilen, haben verschiedene Autoren die Häufigkeit des Fehlens einer
Mehrheitsalternative abzuschätzen versucht. [[19] Vgl. zum Folgenden SEN 1970, S.163ff.] Dabei wurde meist von der Annahme
ausgegangen, dass jede logisch mögliche individuelle Präferenzordnung die gleiche
Wahrscheinlichkeit des Auftretens hat. [[20] So z. B. GARMAN/KAMIEN 1968 und NIEMI/WEISBERG 1968, von
denen die folgenden Ergebnisse stammen.]
Bei Voraussetzung der
Gleichwahrscheinlichkeit beträgt die Wahrscheinlichkeit für das Fehlen einer
Mehrheitsalternative bei 3 Alternativen und 3 Individuen 5,56%. [[21] Siehe SEN 1970, S.164.] Je mehr
Individuen an der Abstimmung teilnehmen, umso größer wird die
Wahrscheinlichkeit für das Fehlen einer Mehrheitsalternative. Jedoch auch bei
unendlich vielen Individuen ist die Wahrscheinlichkeit hierfür niemals größer
als 1:11 oder 8,77%.
Wenn bei einer sehr großen Zahl von Individuen auch
die Zahl der Alternativen ansteigt, dann steigt die Wahrscheinlichkeit für das
Fehlen einer Mehrheitsalternative ständig mit an und überschreitet bei 40
Alternativen mit 81,23% sogar die 80%-Marke, tritt also in mehr als 4 von 5
Fällen auf. [[22] Die Ergebnisse von NIEMI/WEISBERG 1968 finden sich in
SEN 1970, S.164.]{625}
SEN schreibt jedoch dazu: "Dies scheint ein ziemlich
bedrückendes Faktum zu sein. Aber in Wirklichkeit ist es das nicht, denn die
Gleichwahrscheinlichkeitsannahme ist eine sehr spezielle und scheint eine
Nichtberücksichtigung von Gesellschaft in einer bedeutsamen Hinsicht zu
beinhalten. ... Individuelle Präferenzen werden nicht durch die Drehung einer
Roulette-Scheibe über alle möglichen Alternativen bestimmt, sondern durch
bestimmte soziale, ökonomische, politische und kulturelle Kräfte. Dies kann
leicht irgendwelche Muster in der Menge der individuellen Präferenzen
hervorbringen. Das müssen übrigens keine Muster der Übereinstimmung sein.
Scharfe Uneinigkeit kann konsistente und transitive Mehrheits-Entscheidungen
hervorbringen [[23] SEN 1970, S.164f.]
Sofern man jedoch anstelle einer Zufallsverteilung
bestimmte Strukturen bei den individuellen Präferenzordnungen annimmt, so geht
die Wahrscheinlichkeit für das Fehlen einer Mehrheitsalternative zurück oder
verschwindet sogar völlig, wie im Falle der "eingipfligen" Präferenzen.
[[24] Zu eingipfligen Präferenzen s.o. § 111.]
Eine
genauere Einschätzung der praktischen Bedeutsamkeit zyklischer Mehrheiten würde
empirische Untersuchungen über Strukturen und Konstellationen der individuellen
Präferenzen erforderlich machen, die jedoch nur schwer durchzuführen sind.
Da die bisherigen Überlegungen zur Koalitionsbildung und
zum Ausgang der Abstimmung im Mehrheitssystem die Existenz einer
Mehrheitsalternative voraussetzten, sind im Falle des Fehlens einer
Mehrheitsalternative {626} weitergehende Überlegungen erforderlich.
Es stellt
sich die Frage, welches Ergebnis sich bei bestimmten Entscheidungsverfahren wie
z. B. der relativen Mehrheitsregel einstellen wird, wenn keine
Mehrheitsalternative vorhanden ist, die sonst den Gleichgewichtspunkt der
Koalitionsbildung darstellt. Diese Frage soll im Folgenden anhand des obigen
Beispiels zirkulärer Präferenzen aus Abb. 22.1 analysiert werden.
Offenbar reichen in einem solchen völlig symmetrischen Fall
die Kenntnis der individuellen Präferenzordnungen und die Annahme eines
eigeninteressierten Verhaltens der Individuen nicht aus, um das Ergebnis zu
determinieren. Allerdings sind in der Realität die Entscheidungssituationen
praktisch nie vollkommen symmetrisch. Dies ist ebenso unwahrscheinlich wie die
klassische Geschichte vom Esel, der verhungerte, weil er sich nicht entscheiden
konnte, welchen von zwei gleich schmackhaften und gleich weit entfernten
Heubüscheln er fressen sollte.
Zirkuläre Mehrheiten bedeuten, dass es zu jedem möglichen
Ergebnis mindestens ein anderes Ergebnis gibt, das von einer Mehrheit der Individuen
vorgezogen wird. Dadurch gibt es kein stabiles Koalitionsergebnis, denn es
besteht immer die Tendenz, zu einer andern Koalition auf Grundlage einer andern
Vereinbarung überzugehen. Da die Mehrheiten zirkulär sind, ergibt sich im
Prinzip eine endlose Kreisbewegung.
Dies "Koalitionskarussell" mit seinen
verschiedenen Stationen ist in der folgenden Abb. 22.3 wiedergegeben. Dabei sind
die verschiedenen Mehrheits-Koalitionen mit ihrer personellen Zusammensetzung
und der dazugehörigen Koalitionsvereinbarung in der Reihenfolge {627} ihrer Ablösung untereinander geschrieben worden.
"Koalitionskarussell" zu Abb. 22.1
| Koalition aus: | Vereinbarung | |
| 1. Station | A + B | y |
|
Wechsler: |
A | |
| 2. Station | A + C | x |
|
Wechsler: |
C | |
| 3. Station | B + C | z |
|
Wechsler: |
B | |
| 4. Station | B + A | y |
Abb.: 22.3
Damit eine alte Mehrheits-Koalition zugunsten einer neuen
aufgelöst wird, muss immer mindestens ein Individuum von der alten Koalition zur
neuen Koalition wechseln. Es sind diese Wechsler, die gewissermaßen das
Koalitionskarussell in Schwung halten und die verhindern, dass es an einer
bestimmten Stelle zum Stehen kommen kann.
Die Labilität einer bestimmten
Koalition entspricht dabei der Stärke, mit der ein bestimmtes Individuum aus der
einen Koalition in die andere Koalition strebt. Dies hängt jedoch vor allem
davon ab, wie stark seine Präferenzintensität in Bezug auf
das Ergebnis der neuen Koalition gegenüber dem Ergebnis der alten Koalition ist.
Sofern sich interpersonal vergleichbare Unterschiede in den
Präferenzintensitäten der Koalitionswechsler finden, ist die Situation nicht
mehr völlig symmetrisch und bestimmte Koalitionen sind labiler als andere, sodass
sich angeben lässt, welche Koalition in dieser Hinsicht am stabilsten ist und
damit das wahrscheinlichste Endergebnis des Koalitionsbildungsprozesses
darstellt. {628}
Es sei angenommen, dass hinter den Präferenzordnungen der Individuen folgende interpersonal vergleichbare Präferenzintensitäten stehen, die wiederum durch den Abstand zwischen den Alternativen ausgedrückt sind:
Präferenzordnungen (mit Intensitäten)
| A | B | C |
| x | y | z |
| y | - | - |
| - | - | - |
| - | z | x |
| z | x | v |
Abb.: 22.4
Wenn die Präferenzordnungen der Individuen derartig
beschaffen sind, so hat das Koalitionskarussell am wenigsten Schwung beim
Übergang von der Koalition (A + B) auf der Grundlage der Alternative y -
im Folgenden symbolisiert durch "AB:y" - zur Koalition AC:x, denn hier ist A der
erforderliche Wechsler, und für A besteht zwischen den Alternativen x und y nur
eine vergleichsweise geringe Nutzendifferenz.
Demgegenüber sind die beiden
übrigen Koalitionen AC:x und BC:z sehr viel labiler, denn das eine Mal hat
Individuum C ein vergleichsweise starkes Interesse, von x nach z überzugehen,
und das andere Mal hat Individuum B ein ebenso starkes Interesse, von z nach y
überzugehen.
Das Koalitionskarussell wird unter diesen Voraussetzungen
wahrscheinlich bei der Koalition AB:y zum Stehen kommen. Denn Individuum A hat
durch die neue Koalition auf der Grundlage x keine großen Vorteile zu erwarten
und muss außerdem befürchten, dass die neue Koalition mit C nicht sehr stabil sein
wird, da C ein starkes Interesse daran hat, zusammen mit B anstelle von x die
Alternative z durchzusetzen. Dies Ergebnis würde für A jedoch sehr nachteilig
sein, wie aus Abb. 22.4 zu ersehen ist. {629}
Zugleich hat Individuum B im Falle einer Koalition BC:z ein
vergleichsweise starkes Interesse, die Koalition AB:y herzustellen, denn B zieht
y gegenüber z stark vor und B braucht auch seinerseits kaum zu befürchten, dass A
dieser Koalition "untreu" wird, wie die obigen Überlegungen gezeigt haben.
Bei den vorangegangenen Überlegungen ist übrigens nicht
unbedingt davon auszugehen, dass alle Koalitionen tatsächlich geschlossen und
wieder aufgelöst werden. Eher werden die verschiedenen Möglichkeiten von den
Beteiligten in Gedanken durchgespielt und führen dann schließlich zu einer
bindenden Koalitionsvereinbarung. Oder man kann sich die Bestimmung der
stabilsten Koalition so vorstellen, dass dieselbe Konstellation wiederholt
durchgespielt wird nach Art eines Experimentes, sodass die Individuen ihre
strategischen "Fehler" korrigieren können, bis schließlich eine bestimmte
Koalition sich herauskristallisiert als die stabile Lösung.
Noch aus einem andern Grund kann man davon
ausgehen, dass sich eine stabile Lösung auch im Falle zyklischer Mehrheiten
ergibt. Wenn man z. B. davon ausgeht, dass in der Realität immer bereits bestimmte
Koalitionen bestehen, so stellen mögliche Umstellungskosten von
einer bereits bestehenden Koalition auf eine neue Koalition eine "Reibung" dar,
die das Koalitionskarussell ebenfalls bremst. "Der Kern von Stabilität ist nicht
Vollkommenheit sondern Reibung. ... In der Realität entsteht die Reibung aus den
Kosten und Anstrengungen, die erforderlich sind, um genügend politische Kraft
für die Bewirkung einer Änderung aufzubringen." [[25] WINCH 1971, S.187 u. 188.]
Wenn also
{630} neue Koalitionsverhandlungen für die Beteiligten mit Kosten
und möglichen Risiken verbunden sind, so werden sie u. U. selbst dann darauf
verzichten, wenn im Prinzip eine andere Koalitionsvereinbarung auf Grundlage
einer Alternative möglich wäre, die von ihnen bevorzugt wird.
Wenn diese Annahme über Umstellungskosten von einer
Koalition auf die andere zutrifft, so tendiert jede einmal eingegangene
Koalition zur Stabilität. Von dorther gibt es für die Individuen in einer
offenen Koalitionssituation auch ein Motiv, möglichst als erster eine
Koalitionsvereinbarung abzuschließen, um nicht der am schlechtesten gestellte
Dritte zu sein. Neben dem Verhandlungsgeschick der Beteiligten wird dabei
wiederum die relative Präferenzintensität der Individuen in Bezug auf die zur
Entscheidung stehenden Alternativen Auswirkungen darauf haben, welche Koalition
als erste "perfekt" ist.
Dies kann anhand des obigen Beispiels aus Abb. 22.4
verdeutlicht werden. Wenn für Individuum A die Nutzendifferenz zwischen den
Alternativen x und y relativ gering ist, während die Nutzendifferenz zwischen y
und z im Verhältnis dazu sehr groß ist, so wird Individuum A relativ rasch mit
einer Koalition auf der Basis der Alternative y einverstanden sein, um nicht das
Risiko einer Koalition zwischen B und C auf der Basis z einzugehen. Auch unter
diesem Gesichtspunkt würde also die Koalition von A und B auf der Grundlage von
y das wahrscheinlichste Ergebnis sein. {631}
§ 137 Nutzenmäßige Interdependenzen zwischen verschiedenen Entscheidungen im Mehrheitssystem
Wenn eine Reihe von Entscheidungen durch einzelne
Abstimmungen nach dem Mehrheitsprinzip gefällt werden, so kann dabei das
Problem auftreten, dass man die eine Entscheidung sinnvoller Weise nicht
unabhängig vom Ausgang anderer Entscheidungen treffen kann, da die
Konsequenzen der einen Entscheidung die Ausgangsbedingungen der andern
Entscheidung beeinflussen.
So hängt etwa die Entscheidung I, ob die
Verkehrsverbindung zu einer bestimmten Stadt ausgebaut werden sollen oder nicht,
von der Entscheidung II ab, ob diese Stadt Standort eines geplanten großen
Industriewerkes wird oder nicht. Die Abstimmung der Individuen wird folglich bei
der Entscheidung I auch bei identischer Interessenlage unterschiedlich
ausfallen, wenn sie bei der Entscheidung II unterschiedliche Ergebnisse
erwarten.
BLACK nennt solche Interdependenzen zwischen dem
individuellen Nutzen der einen Alternative und der Realisierung einer andern
Alternative aus anderen Entscheidungen "Komplementarität". "Wenn die Rangordnung der Anträge zu einem Gegenstand bei einem
Gremiumsmitglied von Beschlüssen abhängt, von denen es glaubt, dass sie in Bezug
auf einen anderen Gegenstand in Kraft treten werden, so sollen die Anträge
komplementär in Beziehung zu dessen Bewertungen genannt werden. ... Ohne Zweifel
sind sowohl in der Politik als auch in der Ökonomie komplementäre Wertungen die
Regel und unabhängige Wertungen die Ausnahme." [[26] BLACK 1971, S.125.]
{632}
Die Probleme solcher nutzenmäßigen Abhängigkeiten zwischen
verschiedenen Entscheidungen treten allerdings nicht nur bei Anwendung des
Mehrheitsprinzips auf, sondern entstehen generell bei allen Entscheidungen,
sogar bei den isolierten Entscheidungen eines einzelnen Individuums.
Immer wenn
die Ergebnisse der einen Entscheidung I zu den faktischen Ausgangsbedingungen
einer andern Entscheidung II werden, entstehen solche nutzenmäßigen Interdependenzen. Wenn man nicht weiß, wie die Entscheidung I ausfällt, so entsteht
Ungewissheit über die faktische Ausgangslage bei der Entscheidung II.
Wenn die Annahmen der Individuen über das zu erwartende
Ergebnis der Entscheidung I nicht mit dem tatsächlichen Ergebnis übereinstimmen,
so beruhen die Abstimmungen der Individuen bei Entscheidung II auf falschen
faktischen Annahmen, ihre Präferenzäußerungen sind also in dieser Hinsicht
unqualifiziert. Ein Individuum würde in diesem Fall sagen: "Hätte ich gewusst,
dass die Entscheidung I so ausgehen wird, so hätte ich bei der Entscheidung II
anders abgestimmt." BLACK hat die Probleme getrennter Abstimmungen bei Vorliegen
nutzenmäßiger Abhängigkeiten zwischen den einzelnen Entscheidungen näher
analysiert. [[27] S. BLACK 1971, S.125ff. u.
BLACK/NEWING 1951.]
Wenn die Individuen im Falle komplementärer Entscheidungen
die Ergebnisse der andern Entscheidungen nicht kennen, so können kollektive
Fehlentscheidungen auftreten, da die individuellen Präferenzäußerungen
unqualifiziert sind und auf falschen faktischen Annahmen beruhen. Wenn die
Individuen z. B. bei solchen Entscheidungen einzeln aber gleichzeitig abstimmen,
{633} so fehlt ihnen notwendigerweise die Information über den
Ausgang der andern Entscheidung.
Sofern diese Abhängigkeit zwischen den Entscheidungen nur
einseitig ist und man zwar für die Entscheidung II das Ergebnis der Entscheidung
I wissen muss, aber nicht umgekehrt, so lässt sich das Problem durch eine
geeignete Reihenfolge der Abstimmungen lösen. Wenn es z. B. für die Entscheidung
über die Verkehrsplanung wichtig ist zu wissen, welche Entscheidung in Bezug auf
die Industrieansiedlung gefällt wird, kann man zuerst über die
Industrieansiedlung abstimmen und auf der Grundlage des dabei erzielten
Ergebnisses anschließend über die Verkehrsplanung abstimmen. In diesem Fall
ergibt sich also eine "natürliche" Reihenfolge der zu treffenden Entscheidungen,
die auch bei der Anwendung des Mehrheitsprinzips einzuhalten ist, wenn man zu
Ergebnissen kommen will, die einen maximalen Gesamtnutzen darstellen.
Häufig existieren jedoch wechselseitige Abhängigkeiten
zwischen den Entscheidungen: man muss bei Entscheidung I wissen, was das Ergebnis
der Entscheidung II ist, und man muss bei Entscheidung II wissen, was das
Ergebnis bei Entscheidung I ist. Ein solcher Fall kann z. B. vorliegen, wenn sich
die Entscheidung über den Ausbau der Verkehrswege nach der Größe der
Industrieansiedlungen richtet, und wenn sich umgekehrt die Größe der
Industrieansiedlungen nach dem Ausbaustand der Verkehrswege richtet. In einem
solchen Fall müssen beide Entscheidungen "aufeinander abgestimmt" werden.
{634}
Dies kann am besten durch eine Zusammenfassung beider
Entscheidungen zu einer einzigen Entscheidung geschehen, indem jetzt über ein Alternativenbündel abgestimmt wird, das Verkehrsplanung und
industrielle Standortplanung gemeinsam umfasst. Insofern sind für die Lösung des
Problems wechselseitiger Abhängigkeiten zwischen den Entscheidungen Koalitionen
vorteilhaft, da durch sie stabile Mehrheiten für ganze Entscheidungsserien
zustande kommen.
Wenn eine Koalition auf der Grundlage eines bestimmten
Alternativenbündels vereinbart wird, so werden dabei die nutzenmäßigen
Interdependenzen der in diesem Bündel enthaltenen Alternativen automatisch
berücksichtigt.
§ 138 Die Nicht-Berücksichtigung von Präferenzintensitäten durch das Mehrheitsprinzip
1. Intensitätsberücksichtigung bei Einzelentscheidungen
Die unter bestimmten Gesichtspunkten positiv zu wertende
Tatsache, dass bei Anwendung des Mehrheitsprinzips alle Individuen auf die
kollektive Entscheidung einen gleichgewichtigen Einfluss haben, wird dadurch zum
Problem, dass die Interessen der Individuen dabei nur in Form von
Präferenzordnungen, also nutzenmäßigen Rangordnungen der Alternativen
berücksichtigt werden. Für jedes Individuum wird nur festgestellt, ob im
Paarvergleich der Alternativen eine Alternative x besser, gleich gut oder
schlechter ist als irgendeine andere Alternative y. Ausschlaggebend ist dann
allein die größere Zahl derer, die sich für eine der beiden Alternativen
entschieden haben. {635}
SEN illustriert diese Problematik durch ein extremes
Beispiel: "Wenn eine Mehrheit will, dass ich jeden Morgen zwei Stunden lang
Kopfstand mache, dann macht die Methode der Mehrheitsentscheidung dies zu einem
kollektiv bevorzugten Zustand, ganz gleich wie ich diese anspruchsvolle Aussicht
beurteile." [[28] SEN 1970, S.161f. Zur Nicht-Berücksichtigung von
Präferenzintensitäten durch das Mehrheitsprinzip siehe auch die relativ
ausführliche Diskussion bei DAHL 1970, S.48f. und 90ff.]
Wenn Individuum A die Alternative x gegenüber y vorzieht
und Individuum B die Alternative y gegenüber x, so heben sich die Interessen beider Individuen in ihrer
Wirkung auf die kollektive Entscheidung auf. Das Problem ist jedoch,
ob nicht
bei einer genaueren als nur ordinalen Erfassung der individuellen Interessen das
Interesse des Individuums A vielleicht schwerer ins Gewicht fallen würde als das
Interesse des Individuums B.
Wie bereits oben ausgeführt wurde, erfordert das
Solidaritätsprinzip eine möglichst genaue Berücksichtigung der Interessen jedes
Individuums, sodass auch feststellbare interpersonale Unterschiede in den Präferenzintensitäten, also die Größe der Nutzendifferenzen zu
berücksichtigen wären. [[29] Siehe oben § 37.] Wenn für Individuum A die Alternative x sehr viel besser ist als y, während für Individuum B
beide Alternativen nahezu gleichwertig sind, so erscheint bei einer
solidarischen Berücksichtigung der Interessen beider Individuen der Schluss
unzulässig, {636} dass sich die Interessen beider Individuen in ihrer
Bedeutung für das Gesamtinteresse aufheben.
Dies soll nach einmal an einem Beispiel veranschaulicht
werden. Angenommen es geht um die Frage, ob eine bessere Straßenverbindung
gebaut werden soll, wobei allerdings eine Reihe guter Wohnhäuser abgerissen
werden müssten.
Die Alternative x würde (vereinfacht) lauten: "Schlechtere
Verkehrsverbindung bei erhaltenen Wohnhäusern"
und die Alternative y würde
umgekehrt lauten: "Bessere Verkehrsverbindungen bei Abriss der Wohnhäuser".
Die
jetzigen Bewohner der Häuser würden sicherlich die Alternative x gegenüber y
vorziehen, da sie dabei in ihren bisherigen Häusern wohnen bleiben könnten.
Dagegen würden die zukünftigen Straßenbenutzer wahrscheinlich die Alternative y
gegenüber x vorziehen, weil sie dabei Zeit und Wege sparen.
Nach dem
Mehrheitsprinzip würde die Präferenz eines Anwohners durch die Präferenz eines
Straßenbenutzers aufgehoben, und insofern die Straßenbenutzer in der Mehrheit
sind, würde die Alternative x siegen und die Häuser würden zugunsten des
Straßenbaus abgerissen.
Das Mehrheitsprinzip berücksichtigt also nicht den Grad der Betroffenheit verschiedener Individuen durch die Entscheidung. Die Individuen können
die unterschiedliche Gewichtigkeit ihrer Interesse bei einer nur ordinalen
Nutzenbestimmung nicht deutlich machen. Selbst wenn Einigkeit darüber bestünde,
dass der Verlust der eigenen Wohnung für ein Individuum nutzenmäßig sehr viel
schwerer wiegt als eine tägliche Zeitersparnis von einigen Minuten, so könnte
dies im reinen Mehrheitsprinzip nicht berücksichtigt werden. {637}
Das Problem, dass eine existentiell betroffene Minderheit
von einer schwach betroffenen Mehrheit überstimmt werden kann, stellt sich
besonders deshalb verschärft, weil bereits eine knappe Mehrheit von nur einer
Stimme den Ausschlag geben kann, etwa wenn das Abstimmungsergebnis 1000:999
beträgt.
2. Intensitätsberücksichtigung bei Entscheidungsserien
Wie in Kapitel 21 gezeigt wurde, führt das
eigeninteressierte Koalitions- und Abstimmungsverhalten der Individuen im
Mehrheitssystem zu Ergebnissen, die keineswegs einer Anwendung des
Mehrheitsprinzips auf die Einzelentscheidungen entsprechen. Sofern es zu
Globalkoalitionen mit alle Entscheidungen umfassenden Abstimmungsvereinbarungen
kommt, entspricht das Ergebnis stattdessen einer Anwendung des
Mehrheitsprinzips auf globale Alternativenbündel.
Die Frage ist, ob dadurch
das Problem der Berücksichtigung von Präferenzintensitäten bzw.
Nutzendifferenzen gelöst oder doch zumindest gemildert wird.
Durch eine Koalitionsbildung auf der Grundlage von
Alternativenbündeln wird auf jeden Fall die intrapersonale Differenz
der Nutzen in Bezug auf die Einzelalternativen berücksichtigt. So fällt z. B. der
erste Rangplatz einer Einzelalternative bei der Wahl des vorteilhaftesten
Alternativenbündels umso schwächer ins Gewicht, je geringer die Nutzendifferenz zu den übrigen Alternativen dieser Einzelentscheidung ist. Je
nach der intrasubjektiv vergleichbaren Wichtigkeit der Einzelalternativen fallen
diese im Rahmen eines Alternativenbündels {638}auch unterschiedlich ins Gewicht.
Die Frage ist, inwiefern dadurch zugleich eine Berücksichtigung der
interpersonalen Nutzendifferenzen erfolgt.
Dies wäre dann der Fall, wenn man
davon ausgehen könnte, dass die Betroffenheit der Individuen in Bezug auf solche
globalen Alternativenbündel annähernd gleich ist, oder doch zumindest weniger
starke Unterschiede aufweist als die Betroffenheit von den Einzelalternativen.
Die Betroffenheit eines Individuums von einer bestimmten
Entscheidung entspricht seiner Nutzendifferenz zwischen der individuell besten
und der individuell schlechtesten Alternative. Diese Differenz zwischen den
Extremwerten kann man als "Nutzenspannweite" einer Entscheidung für das Individuum
bezeichnen. Die Frage ist, ob die Nutzenspannweiten zwischen den Individuen in
Bezug auf die Alternativenbündel weniger stark variieren als zwischen dem
Durchschnitt der Einzelalternativen. Wenn man einmal Nutzeninterdependenzen
zwischen den Einzelentscheidungen ausschließt, so entspricht die individuelle
Nutzenspannweite der Alternativenbündel der Summe der Nutzenspannweiten der
Einzelalternativen, denn das individuell beste Alternativenbündel ist dann die
Kombination aller Spitzenalternativen des Individuums und das schlechteste
Alternativenbündel ist die Kombination aller schlechtesten Einzelalternativen.
In dem Maße, wie sich die durchschnitt1iche
Nutzenspannweite der Individuen bei den Einzelalternativen angleicht, gleicht
sich damit auch die Nutzenspannweite der Individuen bei den Alternativenbündeln
an. Wenn man also nicht die Annahme {639} macht, dass bestimmte Individuen von sämtlichen
Einzelentscheidungen stärker betroffen sind als andere Individuen, sondern wenn
man davon ausgeht, dass mal die einen und mal die andern Individuen stärker
betroffen sind, so ergibt sich daraus eine Tendenz zur Angleichung der
individuellen Nutzenspannweiten bei den Alternativenbündeln und damit eine
Annäherung des Betroffenheitsgrades der Individuen in Bezug auf die
Gesamtentscheidung zu den Alternativenbündeln.
Diese Überlegung kann noch einmal an einem Beispiel
veranschaulicht werden. Bei Einzelentscheidungen des Kollektivs über bestimmte
Probleme wie Straßenbau, Schulstruktur, Wohnungsbedingungen, Arbeitsbedingungen,
Familienrecht, Besteuerung usw. mag die Betroffenheit der Individuen im
Einzelfall sehr unterschiedlich sein.
So mag einem Individuum A, das selber
keine Kinder im schulpflichtigen Alter hat, die Schulpolitik ziemlich egal sein,
d.h. dass seine Nutzenspannweite zwischen den verschiedenen schulpolitischen
Alternativen nahezu gleich Null ist. Demgegenüber ist ein anderes Individuum B,
das selber Kinder hat, die noch zur Schule gehen, von dieser schulpolitischen
Entscheidung sehr viel stärker betroffen. Bei der Frage der Wohnbedingungen mag
es jedoch genau umgekehrt so sein, dass Individuum A hier unter schlechten
Wohnbedingungen stark leidet, während B hier gut versorgt ist und keine Probleme
hat.
Durch die Bündelung von Einzelentscheidungen aus den verschiedensten
Lebensbereichen mit jeweils unterschiedlicher Betroffenheit der Individuen
ergibt sich dann die Tendenz zu einem Ausgleich der Betroffenheit der Individuen
von der Gesamtentscheidung. {640}
Die berechtigte Kritik am Mehrheitsprinzip, dass es nach
der Maxime 'Ein Individuum, eine Stimme' den Interessen aller Individuen bei
einer Einzelentscheidung gleiches Gewicht gibt, auch wenn die Interessen der
Individuen in Bezug auf diese Entscheidung unterschiedlich gewichtig sind, kann
also nicht ohne weiteres auf das reale Funktionieren eines Mehrheitssystems
übertragen werden, denn hier kommt es zu Koalitionen über ganze
Alternativenbündel und "Programme", die sich aus Einzelentscheidungen auf den
verschiedensten Lebensbereichen zusammensetzen, sodass eine gewisse Angleichung
des Betroffenheitsgrades der Individuen möglich ist.
Mit diesen relativ allgemein gehaltenen Bemerkungen ist
natürlich das Problem der Nicht-Berücksichtigung von Präferenzintensitäten durch
das Mehrheitsprinzip noch keineswegs als gelöst anzusehen. Auch bei der Bildung
von globalen Koalitionen entscheiden allein die nutzenmäßigen Rangplätze der
globalen Alternativenbündel, welches von ihnen die Mehrheitsalternative bildet
und sich durchsetzen wird. Deshalb ist es notwendig, unten im Kapitel 23 noch
einmal Verfahren zur Berücksichtigung von Präferenzintensitäten im
Mehrheitssystem zu erörtern.
§ 139 Mehrheitsalternative und Alternative des größten Gesamtnutzens
In Teil I dieser Arbeit wurde dargelegt, dass allein eine Entscheidung für die Alternative mit dem größten Gesamtnutzen normative Allgemeingültigkeit beanspruchen kann im Sinne einer argumentativen Konsensusfähigkeit. [[30] Siehe dazu oben Kap. 7.] {641} Damit stellt sich die Frage, unter welchen Bedingungen die Mehrheitsalternative auch gleichzeitig die Alternative mit dem größten Gesamtnutzen ist.
Da bei Abstimmungsverfahren im Mehrheitssystem nur die
Präferenzordnungen der Individuen in Bezug auf die zur Entscheidung stehenden
Alternativen bzw. Alternativenbündel eine Rolle spielen, werden die
individuellen Nutzen der Alternativen nur ordinal erfasst, sodass die Bestimmung des Gesamtnutzens der
einzelnen Alternativen, bei dem eine Addition der individuellen Nutzengrößen
notwendig ist, auf dem Wege der Mehrheitsabstimmung nicht geleistet werden kann.
[[31] Zur Bestimmung des Gesamtnutzens s.o. § 39.] Trotzdem lässt sich allgemein angeben,
unter welchen
Annahmen hinsichtlich der individuellen Nutzenfunktionen die
Mehrheitsalternative mit der Alternative des maximalen Gesamtnutzens identisch
ist.
Dies kann anhand der Präferenzordnungen von 5 Individuen A
bis E in Bezug auf die 2 Alternativen x und y verdeutlicht werden:
Präferenzordnungen
| A | B | C | D | E |
| y | y | x | x | x |
| x | x | y | y | y |
Abb.: 22.5
Die Mehrheitsalternative ist in diesem Fall die
Alternative x. Um festzustellen, ob x auch die Alternative mit dem größten
Gesamtnutzen ist, müsste man die individuellen Nutzen für beide Alternativen bestimmen,
{642} addieren und vergleichen.
Da sich der Gesamtnutzen
einer Alternative aus der Summe der individuellen Nutzen und damit aus dem
Produkt aus "Anzahl der Individuen" mal dem "durchschnittlichen individuellen
Nutzen" ergibt, kann man auch sagen, dass die Mehrheitsalternative dann den
größten Gesamtnutzen aller Alternativen hat, wenn bei ihr der durchschnittliche
individuelle Nutzen am größten ist.
Anstelle der individuellen Nutzen kann man
auch die Nutzendifferenzen zur Bestimmung der nutzenmaximalen Alternative
verwenden. Dann müssen die durchschnittlichen individuellen Nutzendifferenzen
zwischen der Mehrheitsalternative und jeder andern Alternative absolut gesehen
bei den Befürwortern der Mehrheitsalternative mindestens ebenso groß sein wie
bei den Gegnern der Mehrheitsalternative, damit die Mehrheitsalternative
zugleich die Alternative des größten Gesamtnutzens ist.
Eine ähnliche Feststellung treffen auch BUCHANAN und
TULLOCK. "Wenn angenommen wird, dass alle individuellen Präferenzen von gleicher
Intensität sind, wird durch die einfache Mehrheitsregel garantiert, dass die
aufsummierten 'Vorteile' (benefits) der Entscheidung die summierten 'Verluste'
(losses) übersteigen werden. ... Wenn jedoch die individuellen
Präferenzintensitäten nicht für alle Wähler gleich sind, verschwindet dieser
besondere Zug der einfachen Mehrheitsregel." [[32] BUCHANAN/TULLOCK 1969, S.126f.]
Allerdings ist diese
Formulierung nicht ganz korrekt, denn die Mehrheitsregel führt auch bei
ungleichen Präferenzintensitäten der Individuen auf jeden Fall zur Auswahl der
Alternative {643} mit dem größten Gesamtnutzen, sofern nur die
durchschnittliche Präferenzintensität bei den Mitgliedern der Mehrheit ebenso
groß oder größer ist als bei den Mitgliedern der unterlegenen Minderheit.
Dies wird auch von DAHL betont, der Mehrheitsentscheidungen je nach der
Beschaffenheit der Präferenzintensitäten bei Mehrheit und Minderheit
klassifiziert und diskutiert. Nach DAHL muss auch bei unterschiedlichen
Präferenzintensitäten die Anwendung der Mehrheitsregel nicht ethisch
problematisch sein, denn "in diesen Fällen enthält die Mehrheit ... mindestens ebenso viele Individuen, die stark für oder gegen eine Politik sind, wie die
Minderheit." [[33] DAHL 1970, S.94.]
Problematisch ist nach DAHL nur eine Konstellation, die er "schwere asymmetrische Uneinigkeit" nennt, "wo eine große Minderheit eine starke
Präferenz für eine von zwei Alternativen hat und die dagegen stehende Mehrheit
nur eine schwache Präferenz für die andere hat. [[34] DAHL 1970, S.99.]
Wie oben festgestellt wurde, kann die Mehrheitsalternative
nur dann nicht den maximalen Gesamtnutzen besitzen, wenn die durchschnittliche
Präferenzintensität der Minderheit bei einer der konkurrierenden Alternativen
größer ist als die der Mehrheit.
Aber selbst in diesem Fall kann die
Mehrheitsalternative weiterhin die Alternative mit dem größten Gesamtnutzen
sein, sofern nur die Mehrheit entsprechend zahlenmäßig überlegen ist. Dies kann
anhand des obigen Beispiels aus Abb. 22.5 veranschaulicht werden, indem einmal
fiktive Nutzenwerte angenommen {644} werden:
Präferenzordnungen (mit Nutzenwerten)
| A | B | C | D | E |
| y(10) | y(10) | x(10) | x(10) | x(10) |
| x(6) | x(6) | y(7) | y(7) | y(7) |
Abb.: 22.6
In diesem Beispiel ist die Mehrheit von 3 Individuen (C, D
und E) für die Alternative x und die Minderheit von 2 Individuen (A und B) für
y. Wie man sieht, ist in diesem Fall die Präferenzintensität der Minderheit mit
4 Nutzeneinheiten größer als die Präferenzintensität der Mehrheit mit 3
Nutzeneinheiten. Trotzdem hat hier die Mehrheitsalternative x mit 42
Nutzeneinheiten immer noch einen größeren Gesamtnutzen als die
Minderheits-Alternative y mit 41 Nutzeneinheiten. Durch die zahlenmäßige
Überlegenheit der Mehrheit kann also eine stärkere Präferenzintensität der
Minderheit wieder wettgemacht werden.
Allgemein kann man sagen, dass die Mehrheitsalternative
immer dann auch die Alternative mit dem größten Gesamtnutzen ist, wenn gilt,
dass
das zahlenmäßige Verhältnis zwischen der Mehrheit und der Minderheit größer ist
als das Verhältnis zwischen der durchschnittlichen Präferenzintensität der
Minderheit und der der Mehrheit.
In unserm Beispiel war das zahlenmäßige
Verhältnis von Mehrheit zu Minderheit 3:2 und das Verhältnis zwischen den
durchschnittlichen Präferenzintensitäten von Minderheit und Mehrheit 4:3. Da 3:2
größer ist als 4:3, muss in diesem Fall die Mehrheitsalternative zugleich auch
den maximalen Gesamtnutzen besitzen.{645}
Ob bei Anwendung des Mehrheitsprinzips tatsächlich
die Alternative des größten Gesamtnutzens gewählt wird, kann also im Einzelfall
auch von der zahlenmäßigen Überlegenheit der Mehrheit gegenüber der Minderheit
abhängen.
Dadurch wird die weitverbreitete Anschauung verständlich, dass die
Legitimation einer Mehrheitsentscheidung umso stärker ist, je größer das
zahlenmäßige Gewicht dieser Mehrheit ist. Die Existenz dieser Auffassung stützt
die in dieser Arbeit gemachte Annahme, dass auch bei der Legitimation von
Abstimmungen nach dem Mehrheitsprinzip quantitative Nutzenvorstellungen im
Hintergrund stehen, obwohl in der Abstimmung selber nur die ordinalen
Nutzenwerte zum Ausdruck kommen. Andernfalls müsste in Bezug auf die normative
Anerkennbarkeit Mehrheitsentscheidung gleich Mehrheitsentscheidung sein,
gleichgültig ob die Mehrheit das eine Mal "hauchdünn" und das andere Mal "überwältigend" war. {646}
23. Kapitel
Verfahren zur
Berücksichtigung der Präferenzintensitäten im
Mehrheitssystem
§ 140 Die Anhebung der erforderlichen Mehrheit
Da das Mehrheitsprinzip auf nur ordinalen individuellen
Nutzen basiert, können interpersonale Unterschiede der Präferenzintensitäten
nicht erfasst werden. Unter dem Gesichtspunkt einer Maximierung des Gesamtnutzens
ist dies die zentrale Schwäche des Mehrheitsprinzips. Es sind jedoch Verfahren
denkbar, die unter Ergänzung oder Modifizierung des Mehrheitsprinzips eine
Berücksichtigung von Präferenzintensitäten ermöglichen.
Um sicherzustellen, dass die kollektiv gewählte Alternative
auch dann noch die Alternative des größten Gesamtnutzens ist, wenn die
durchschnittliche Präferenzintensität der Minderheit größer ist als die der
Mehrheit, könnte man fordern, dass die gewählte Alternative nicht nur von einer
relativen oder absoluten Mehrheit gegenüber jeder anderen Alternative vorgezogen
wird, sondern von einem höheren Anteil der Individuen, z. B. mehr als zwei
Dritteln oder mehr als drei Vierteln. Dann wäre die derart qualifizierte
Alternative, die man als "Zwei-Drittel-Alternative" bzw. "Drei-Viertel-Alternative" bezeichnen könnte, auf jeden Fall noch die
Alternative des größten Gesamtnutzens, selbst wenn die durchschnittliche
Präferenzintensität der Mehrheit nur 1/2 bzw. 1/3 so groß wäre wie die der
Minderheit. {647}
Diese Eigenschaft qualifizierter Mehrheitsregeln, wie diese auch genannt werden, kann an einem Beispiel nach der Regel der Zwei-Drittel-Mehrheit veranschaulicht werden, bei der 3 interessemäßig in sich homogene Gruppen zwischen den 3 Alternativen x, y und z abstimmen. (Die Anzahl der Individuen und die individuellen Nutzenwerte sind in Klammern gesetzt.)
Präferenzordnungen mit Nutzenwerten für 3 Gruppen
| A (9) | B (9) | C (11) |
| x (30) | z (18) | y (30) |
| y (20) | y (10) | y (26) |
| z (16) | x (5) | x (25) |
Abb.: 23.1
Die dazugehörige Wahlmatrix sieht folgendermaßen aus:
Wahlmatrix zu Abb. 23.1
| x | y | z | |
| x | - | 9:20 | 9:20 |
| y | 20:9 | - | 20:9 |
| z | 20:9 | 9:20 | - |
Abb.: 23.2
Wie man sieht, ist hier die Alternative y jeder anderen
Alternative mit 2/3 Mehrheit überlegen. In diesem Fall könnte die
durchschnittliche Präferenzintensität in Bezug auf y gegenüber x und gegenüber z bei den jeweiligen Befürwortern von y sogar nur halb so
groß sein wie bei den jeweiligen Gegnern von y, denn es gibt in jedem
Paarvergleich mehr als doppelt soviel Befürworter wie Gegner von y.
In unserm Beispiel aus Abb. 23.1 bestehen folgende
durchschnittliche Nutzendifferenzen bei der Zwei-Drittel-Mehrheit {648} und bei der Minderheit:
Durchschnittliche individuelle Nutzendifferenzen zu Abb. 23.1
| y und x | y und z | |
| 5 | 4 | bei den Befürwortern von y (2/3-Mehrheit) |
| 10 | 8 | bei den Gegnern von y (Minderheit) |
Abb.: 23.3
Obwohl in diesem Fall die Minderheit von der Entscheidung sehr viel stärker betroffen ist, bleibt y mit 600 Nutzeneinheiten immer noch die Alternative mit dem größten Gesamtnutzen, wie die folgende Aufstellung des Gesamtnutzens für alle Alternativen zeigt:
Gesamtnutzen von x = (9 x 30) + (9 x 5) + (11 x 25) = 470
Gesamtnutzen von y = (9 x 20) + (9 x 10) + (11 x 25) = 600
Gesamtnutzen von z = (9 x 16) + (9 x 18) + (11 x 26) = 592.
Je höher der erforderliche Anteil der Befürworter der
siegreichen Alternative gegenüber jeder andern Alternative gesetzt wird, desto
stärker darf die Präferenzintensität der überstimmten Minderheit im Verhältnis
zur durchschnittlichen Präferenzintensität der Mehrheit werden, ohne dass die
siegreiche Alternative ihre Eigenschaft als Alternative des größten
Gesamtnutzens verliert.
Im Extremfall, wo eine Mehrheit von 100% der Individuen
gegenüber jeder andern Alternative gefordert wird, wo die siegreiche {649} Alternative also einstimmig für besser gehalten
werden muss als jede andere Alternative, spielen mögliche Unterschiede der
individuellen Präferenzintensitäten überhaupt keine Rolle mehr, da es nur noch
Befürworter der siegreichen Alternative gibt. Bei Anwendung einer derartigen
Einstimmigkeits-Regel kann man sicher sein, dass eine erfolgreiche Alternative
zugleich immer die Alternative des höchsten Gesamtnutzens ist. [[1] Zu den Einstimmigkeits-Regeln s.o. Kap.12. Da hier die
Präferenzintensitäten keine Rolle spielen, bot sich dies Kriterium für die
ordinalistische Paretianische Wohlfahrtsökonomie an, die ohne interpersonale
Nutzenvergleiche auskommen will. Allerdings erfährt die Einstimmigkeits-Regel
durch die Eigentumsrechte entscheidende Veränderungen.]
Je höher der geforderte Anteil von Befürwortern
für die kollektiv gewählte Alternative gesetzt wird, desto größer ist die
Wahrscheinlichkeit, dass überhaupt keine der Alternativen dem Kriterium genügt.
Wenn eine Zwei-Drittel-Mehrheit gefordert wird, dann muss eine erfolgreiche
Alternative im paarweisen Vergleich gegenüber jeder andern Alternative
mindestens doppelt so viel Stimmen bekommen wie die konkurrierende Alternative,
und bei einer Drei-Viertel-Mehrheit sogar dreimal so viel.
Es würde
wahrscheinlich häufig der Fall eintreten, dass keine der Alternativen dem
Kriterium derart qualifizierter Mehrheiten genügt, sodass die Entscheidungs-Regel
unvollständig ist und es zu gar keiner Entscheidung kommt. [[2] Übrigens setzen sich vorhandene
qualifizierte
Mehrheitsalternativen ähnlich wie einfache Mehrheitsalternativen bei rationaler
Koalitionsbildung auch bei einmaligen Abstimmungen durch.] {650}
Wenn man nun für solche Fälle eine Status-quo-Klausel
einführt, so entsteht dadurch eine Bevorzugung der bestehenden Verhältnisse und
eine konservative Schlagseite des Entscheidungsverfahrens, die sich umso stärker
auswirkt, je höher der geforderte Mehrheitsanteil gesetzt wird. Die
Konsequenzen solcher Status-quo-Klauseln wurden anhand der
Einstimmigkeits-Regeln bereits ausführlich erörtert. [[3] Zur Status-quo-Klausel s.o. § 71.]
Die Probleme liegen hier
ähnlich, denn durch die Status-quo-Klauseln wandeln sich die qualifizierten
Mehrheitsregeln zu Minderheits-Veto-Regeln. Die Regel der Zwei-Drittel-Mehrheit
mit Status-quo-Klausei muss deshalb richtiger "Ein-Drittel-Veto-Regel" heißen,
denn es handelt sich hier um Varianten der Veto-Regel. Man spricht deshalb hier
auch von Sperr-Minoritäts-Regeln.
Bei diesen Sperr-Minoritäts-Regeln haben nicht mehr alle
Individuen gleichen Einfluss auf die kollektive Entscheidung, denn ein Individuum
der Sperrminorität hat ein größeres Gewicht bei der Durchsetzung des Status quo
als ein Individuum der relativen Mehrheit, die erfolglos gegen den Status quo
zugunsten einer andern Alternative votiert. Veto-Regeln sind gegenüber den
Alternativen nicht neutral, da der Status quo bevorzugt wird. [[4] Siehe dazu oben § 120.]{651}
§ 141 Die Einführung individueller Abstimmungskosten
Häufig ist die Abstimmung für ein Individuum mit bestimmten
Kosten verbunden, die vor allem in der Form des Zeitaufwands auftreten. In
diesem Fall wird ein eigeninteressiertes Individuum an der Abstimmung dann nicht
teilnehmen, wenn die individuelle Nutzenspannweite zwischen bester und
schlechtester Alternative geringer ist als der individuelle Abstimmungsaufwand.
Denn selbst im günstigsten Fall, wenn die Spitzenalternative des Individuums
durch dessen Stimmabgabe die erforderliche Mehrheit erhält, überwiegen die
Nachteile der Abstimmung die Vorteile des Ergebnisses für das betreffende
Individuum.
Abstimmungskosten stellen also eine Schwelle dar, die
solche Individuen von der Beteiligung an der Abstimmung abhält, die den zur
Entscheidung stehenden Alternativen weitgehend indifferent gegenüberstehen, die
also nur eine sehr geringe Präferenzintensität in dieser Frage besitzen. Dadurch
werden diejenigen Individuen, die von der anstehenden Entscheidung kaum
betroffen sind, automatisch von der Abstimmung ferngehalten, und es verringert
sich die Gefahr, dass eine "laue" Mehrheit eine "engagierte" Minderheit
überstimmt.
Allerdings ist der Rückschluss von der Nicht-Teilnahme an
der Abstimmung auf die geringe Betroffenheit des Individuums von der
Entscheidung nicht unbedingt zulässig. Abgesehen von der Möglichkeit
irrationaler politischer Apathie und von der generellen Frage, ob die Individuen
überhaupt hinreichend über ihre Interessenlage aufgeklärt sind, muss geprüft
werden, {652} ob bestimmte Abstimmungskosten - etwa in Form einer
Teilnahme an mehrstündigen Versammlungen, an deren Ende die Abstimmung
stattfindet - auch für alle Individuen vergleichbare Abstimmungskosten
beinhaltet, oder ob nicht für einige Individuen die Teilnahme an der Versammlung
einen vergleichsweise größeren Aufwand darstellt als für andere Individuen.
Man
denke etwa an eine Situation, wo ein Teil der Individuen Kinder zu versorgen
hat, sodass deren Zeit verhältnismäßig knapper ist als die der andern Individuen.
In ähnlicher Weise kann auch eine gleiche Abstimmungsgebühr für die Individuen
ein unterschiedlich großes Opfer bedeuten. [[5] Siehe dazu oben §§ 115 u. 46]
Weiterhin spielt für ein eigeninteressiertes Individuum nicht nur seine Nutzenspannweite eine Rolle bei der Entscheidung darüber, ob es an der Abstimmung teilnehmen soll oder nicht. Von entscheidender Bedeutung ist es dabei, ob das Individuum der Ansicht ist, dass die eigenen Stimmabgabe einen Einfluss auf das Endergebnis haben wird oder nicht. [[6]Zur Auswirkung von Abstimmungskosten s. DOWNS 1968, S.260ff.]
Wenn ein Individuum z. B. der
Ansicht ist, dass die von ihm bevorzugte Alternative sowieso die Mehrheit
bekommen wird, so wird es die Kosten der Abstimmung scheuen, selbst wenn seine
Präferenzintensität relativ groß ist. Dasselbe gilt für alle Fälle, in denen das
Ergebnis der Abstimmung für das Individuum von vornherein festzustehen scheint.
Vor allem in sehr großen Kollektiven wird die Überlegung für eigeninteressierte
Individuen eine große Rolle spielen, dass die eigene Stimme sowieso keinen
entscheidenden Einfluss auf das Ergebnis haben wird und man deshalb lieber die
Kosten der {651} Abstimmung spart.
Damit stellt sich hier ein ähnliches "Trittbrett-Fahrer-Problem" wie bei öffentlichen Gütern im Eigentum-Vertrags-System. [[7]
Zu kollektiven Gütern s.o. § 92.] Man kann nämlich den Abstimmungssieg einer bestimmten
Alternative als ein kollektives Gut auffassen, das allen Individuen
mit entsprechender Interessenlage zugute kommt, gleichgültig ob sie nun an der
Abstimmung teilgenommen haben oder nicht. Bei Existenz von individuellen
Abstimmungskosten kann es deshalb für ein eigeninteressiertes Individuum die
vorteilhafteste Strategie sein, durch Nicht-Teilnahme an der Abstimmung Kosten
zu sparen und trotzdem aufgrund der Abstimmung anderer an den Vorteilen der
durchgesetzten Alternative teilzuhaben.
Wenn allerdings jeder so denken und handeln würde, so würde
eine Alternative bei der Abstimmung unterliegen, obwohl sie von der
überwiegenden Mehrheit der Individuen bevorzugt wird, nur weil ihre Anhänger die
individuellen Kosten der Abstimmung gescheut haben und sich auf die Teilnahme
der jeweils anderen verlassen haben. Aus diesem Grund stellt die bewusste
Einführung individueller Abstimmungskosten als Barriere gegenüber indifferenten
Individuen ein zweifelhaftes Mittel zur Berücksichtigung von
Präferenzintensitäten im Mehrheitssystem dar.
Insofern die zur Entscheidung stehenden Alternativen den
Charakter kollektiver Güter haben, von deren {653} Nutzen niemand gezielt ausgeschlossen werden kann, bedeutet
jede Erhöhung der individuell anfallenden Abstimmungskosten eine Verschärfung
des Trittbrett-Fahrer-Problems. Zu dessen Lösung erscheint also umgekehrt eine
Minimierung der individuellen Abstimmungskosten geboten sowie die Formulierung
einer moralischen oder sogar rechtlich sanktionierten Pflicht zur Teilnahme an
der Abstimmung. [[8] Der Umstand, dass es bei Mehrheits-Abstimmungen um
kollektive Güter gehen kann, ist übrigens ein weiterer Grund gegen den
Stimmenkauf, weil dabei Individuen versuchen könnten, doppelt zu "kassieren" :
durch Verkauf ihrer Stimme und durch das Endergebnis.]
§ 142 Die Einrichtung kollektiver oder individueller Verfügungsbereiche
Ein Verfahren zur Ergänzung des Mehrheitsprinzips, das
sowohl eine Verringerung des Entscheidungs-Aufwands als auch eine
Berücksichtigung der Präferenzintensitäten gestattet, ist die Einrichtung
separater Verfügungsbereiche. [[9] Siehe dazu oben §§ 64 u. 80.] Dabei werden für
einen bestimmten Entscheidungsbereich nur die vor allem davon betroffenen
Individuen zu einem Teilkollektiv zusammengefasst und diesem Teilkollektiv wird
die Zuständigkeit für diesen Bereich übertragen. Dadurch sind die weniger
betroffenen Individuen von der Entscheidung ausgeschlossen, sodass es nicht
möglich ist, dass eine selber kaum betroffene Mehrheit eine stark betroffene
Minderheit überstimmt.
Je nach der Art der Entscheidungsbereiche kann diese
Untergliederung in dezentral entscheidende Teilkollektive {655} nach den unterschiedlichsten Kriterien vorgenommen
werden und kann unterschiedlich fein gegliedert sein, von Territorial-Staaten,
über föderale Untergliederungen und Gemeinden bis hin zu den einzelnen
Individuen, die in Fragen, die vor allem sie selber betreffen, das alleinige
Verfügungsrecht erhalten. Dadurch unterteilt sich die Gesamtheit aller
Individuen in eine Vielzahl von Teilkollektiven, denen jeweils bestimmte, vor
allem sie selber betreffende Entscheidungskomplexe zur autonomen Entscheidung
überlassen sind.
Dabei kann natürlich ein einzelnes Individuum ohne weiteres
Mitglied in verschiedenen Teilkollektiven sein. Es kann z. B. zugleich als
Mitglied des Staates, der Gemeinde, des Betriebes, der Familie oder als Nutzer
eines Wirtschaftsbetriebes sein Interesse artikulieren.
Zur Funktionsfähigkeit eines solchen untergliederten
Systems, dessen Teilkollektive jeweils nach dem Mehrheitsprinzip entscheiden,
bedarf es einmal einer Regelung der Zuständigkeit der verschiedenen
Teilkollektive für die auftretenden Entscheidungen, und es bedarf außerdem einer
Zuordnung der Individuen zu den verschiedenen Teilkollektiven. Die
dabei auftretenden Probleme einer Abgrenzung der Verfügungsbereiche und einer
Einschätzung des Betroffenheitsgrades der Individuen sollen hier jedoch nicht
weiter verfolgt werden, da sie bereits oben angesprochen wurden.
Auch hier
gelten übrigens wieder die Vorteile der Dezentralisierung durch eine bessere
Information der Individuen über die zu treffenden Entscheidungen und durch eine größere Motivation zur Qualifikation der eigenen Interessenäußerung, die
bereits oben in § 81 erörtert wurde. {656}
Die Einrichtung separater Verfügungsbereiche mit relativ autonomen Teilkollektiven scheint das am besten geeignete Mittel zu sein, um die Schwächen des Mehrheitsprinzips auszugleichen. Eine derartige Dezentralisierung der Entscheidungen kann sowohl den Informations-und Entscheidungsaufwand radikal senken, als auch die Voraussetzungen für eine annähernd gleiche Betroffenheit aller Abstimmungsberechtigten von den zu treffenden Entscheidungen schaffen. {657}
24. Kapitel
Zusammenfassung und
Schluss
§ 143 Zusammenfassung und Schluss
Zum Abschluss soll noch einmal der insgesamt durchlaufene
Gedankengang zusammengefasst werden, um den erreichten Stand zu markieren, von
dem aus weitere Untersuchungen durchzuführen wären.
Ausgangspunkt war das Ungenügen an der Beschränktheit des
positivistischen Erkenntnisprogramms und die Forderung, auch in Bezug auf
normative bzw. werthaltige Fragen methodisch gesicherte, allgemeingültige
Antworten zu suchen. Die Absicht war also, neben der positiven Wissenschaft auch
die methodischen Grundlagen für eine normative Wissenschaft zu klären bzw. die
dazu bereits vorhandenen Ansätze fortzuführen. Damit war die Aufgabe gestellt,
analog zur bereits hochentwickelten Methodologie der Erfahrungswissenschaften
eine entsprechende Methodologie für die normativen Wissenschaften zu entwickeln,
anhand derer sich Fragen nach dem was sein soll, allgemeingültig beantworten
lassen.
Ohne eine derartige normative Methodologie müsste jede Kritik oder
Rechtfertigung gesellschaftlicher Ordnungen im Zustand bloß subjektiver
Meinungsäußerungen verbleiben, die vielleicht mit viel rhetorischer Kunst und
großem Engagement vorgetragen sein mögen, denen jedoch die Eigenschaft
zwingender Argumentation fehlt.
Die erkenntnistheoretische Basis für eine derartige
normative Methodologie im Sinne einer "Lehre von den Methoden zur
allgemeingültigen {658} Beantwortung normativer Fragen" findet sich in den
notwendigen Voraussetzungen jeder Argumentation einschließlich der Argumentation
für und wider normative Behauptungen.
Diese Voraussetzungen formuliert das
Intersubjektivitätsgebot, das alle Beteiligten an der
Auseinandersetzung um Behauptungen mit dem Anspruch auf Allgemeingültigkeit
darauf verpflichtet, nach einem argumentativen Konsensus zu
streben, der nur durch Vernunftgründe und unter Ausschluss jeder Form von Gewalt
herstellbar sein muss.
Diese allgemeinen Voraussetzungen der Argumentation können
nun zwar bestimmte Pseudo-Argumentationen auf normativem Gebiet eliminieren,
aber das Intersubjektivitätsgebot, das ja für alle Formen allgemeingültiger
Erkenntnis gilt, ist als Kriterium noch nicht hinreichend, um normative
Streitfragen zu entscheiden. Es bedarf analog zum Erfahrungskriterium in den
positiven Wissenschaften, das dort einen gewaltfreien intersubjektiven Konsensus
ermöglicht, eines entsprechenden Kriteriums für die normativen Wissenschaften.
Dieses Kriterium, das einen gewaltfreien Konsensus in
normativen Fragen ermöglicht, bildet das Solidaritäts-Prinzip, das von jedem Teilnehmer einer normativen Argumentation verlangt, bei der
Bestimmung allgemeingültiger Normen das Interesse jedes andern Individuums so zu
berücksichtigen, als wäre es sein eigenes Interesse.
Während der Dissens in
positiven Fragen im Kern auf eine unterschiedliche Wahrnehmung der Wirklichkeit
zurückgeht und durch das Kriterium intersubjektiv nachvollziehbarer Erfahrung im
Prinzip vernünftig {659} auflösbar ist, handelt es sich beim Dissens in normativen
Fragen im Kern um einen unterschiedlichen Willen in Bezug auf die Wirklichkeit. Ein solcher willensmäßiger Dissens ist nur
durch den Bezug auf das Kriterium der intersubjektiven
Nachvollziehbarkeit der individuellen Interessen und ihrer solidarischen Zusammenfassung zu einem Gesamtinteresse vernünftig auflösbar.
Ähnlich wie das Kriterium der Beobachtbarkeit in seiner
allgemeinen Form jedoch noch nicht hinreicht, um über die Wahrheit sämtlicher
Behauptungen hinsichtlich der Beschaffenheit der Wirklichkeit zu befinden - man
denke etwa an Behauptungen über Vorgänge auf dem Mars, über den inneratomaren
Bereich oder über innerpsychische Prozesse, deren Überprüfung erst die
Entwicklung eines geeigneten Beobachtungsinstrumentariums
voraussetzt -, so bedarf auch das Solidaritäts-Prinzip einer Umsetzung in
geeignete Verfahren der Interessenermittlung auf den verschiedenen Bereichen.
Auf diesem Bereich der interpersonal vergleichbaren Nutzenmessung liegen noch große
Probleme, die in dieser Arbeit nur ansatzweise gelöst werden konnten.
Im Folgenden wurden dann konkrete Verfahren der
Interessenermittlung und ihrer Zusammenfassung unter dem Gesichtspunkt des
Solidaritätsprinzips analysiert.
Wenn man sich auf individualistische
Entscheidungsverfahren beschränkt, in denen jedes Individuum seine Interessen
selbst bestimmt, so erscheinen vor allem zwei Grundmodelle der kollektiven
Entscheidung von Bedeutung: einmal das Eigentum-Vertrags-System, in dem Entscheidungen gefällt bzw.
Normen gesetzt werden durch Märkte, {660} die nach dem Tausch-Prinzip funktionieren, und zum andern
das Mehrheitssystem, in dem Normen gemäß dem Willen der in
Abstimmungen erfolgreichen Mehrheiten gesetzt werden.
Die Auswahl dieser beiden Verfahren der Normsetzung
rechtfertigt sich daraus, dass sie die Kernstrukturen der industrialisierten
Gesellschaften des kapitalistisch-parlamentarischen Typs darstellen. "In
kapitalistischen Demokratien gibt es im wesentlichen zwei Methoden, durch die
Entscheidungen gefällt werden können: die Abstimmung, die typischerweise für
'politische' Entscheidungen benutzt wird, und der Marktmechanismus, der
typischerweise für 'ökonomische' Entscheidungen benutzt wird." [[1] ARROW 1963, S.1.]
Außerdem lassen
sich die großen politischen Richtungen der Gegenwart vor allem danach
charakterisieren, inwiefern sie die kollektiven Entscheidungen einer
industrialisierten Gesellschaft eher dem Marktmechanismus oder eher einem
Wahlmechanismus übertragen wollen, wenn man einmal von den Befürwortern autoritärer
Entscheidungs-System stellvertretender Herrschaft absieht.
Wie aus den Ausführungen deutlich geworden ist, stellen
weder das Eigentum-Vertrags-System noch das Mehrheitssystem 'letzte Werte' dar,
wie es manchmal den Anschein hat, etwa wenn die Wahl zwischen beiden Formen
gesellschaftlicher Willensbildung als 'Wahl zwischen den Grundwerten Freiheit
und Gleichheit' interpretiert wird. Stattdessen müssen Märkte und Abstimmungen
als Normsetzungsverfahren in den allgemeinen Rahmen einer normativen
Methodologie gestellt werden, um von dort aus auf ihre Legitimation geprüft {661}zu werden.
Unter dem Gesichtspunkt des Solidaritäts-Prinzips
können beide Verfahren keine obersten Maßstäbe sein, sondern sind nur als mehr
oder weniger geeignete Annäherungsverfahren zur Bestimmung allgemeingültiger
Normen bzw. zur Realisierung des Gesamtinteresses anzusehen.
Es handelt sich bei diesen Verfahren schon insofern um
Annäherungsverfahren, als die Bestimmung der individuellen Interessen den
Betroffenen selbst überlassen bleibt. Damit steht und fällt die Legitimation
beider Verfahren jedoch mit der Fähigkeit der Individuen, ihre eigenen
Interessen richtig bestimmen zu können.
Ebenso kann
die im Eigentum-Vertrags-System praktizierte Beschränkung der individuellen
Interessen auf den eigenen Eigentumsbereich sowie ihre Gewichtung entsprechend
dem Einkommen höchstens als eine Annäherung an eine solidarische
Berücksichtigung aller individuellen Interessen gerechtfertigt werden, jedoch
keineswegs einen letzten normativen Maßstab abgeben. Entsprechendes gilt für das
Mehrheitssystem, in dem die individuellen Interessen nur ordinal erfasst werden
und dann gleichgewichtig behandelt werden.
Hinsichtlich der Überlegenheit des einen oder des andern
Systems muss jedoch vor voreiligen Schlussfolgerungen gewarnt werden. Als erstes
ist festzustellen, dass es keine pauschale Alternative zwischen dem
Eigentum-Vertrags-System und dem Mehrheitssystem geben kann, da die
verschiedenartigsten Kombinationen beider Systeme möglich sind, je nach der
Ausdehnung des privaten Eigentumsbereichs. Wie aus den obigen Erörterungen
deutlich wird, hängt es immer von bestimmten, Bedingungen ab, wie {662} gut oder wie schlecht das jeweilige System die Annäherung
an das Gesamtinteresse vollzieht.
So wird die Anwendung des Eigentum-Vertrags-Systems unter
normativen Gesichtspunkten umso problematischer, je ungleicher Vermögen und Einkommen auf die Individuen verteilt
sind, je stärker die Interdependenzen zwischen den Eigentumsbereichen sind und
je ungleicher die Verhandlungsmacht der Individuen aufgrund von Monopolbildung
ist.
Andererseits ist die Anwendung des Mehrheitssystems umso problematischer,
je größer die Unterschiede in der Betroffenheit der Individuen sind, je
zahlreicher und komplexer die zu entscheidenden Probleme sind und je geringer
die Eigenmotivation der Individuen zur Befolgung der Mehrheitsbeschlüsse ist.
Es wird deshalb keine pauschale Entscheidung für das eine
oder das andere System geben können, sondern man wird je nach
Entscheidungsbereich und nach der Art der dort vorliegenden Bedingungen das
besser geeignete Verfahren anwenden müssen, sodass ein aus beiden Systemen
gemischtes Gesamtsystem entsteht. Weil dabei die konkreten
Ausgangsbedingungen berücksichtigt werden müssen, kann es folglich kein
für alle Zeiten und Länder bestes ökonomisches oder politisches System geben.
Außerdem muss im Auge behalten werden, dass
Eigentum-Vertrags-System und Mehrheitssystem in der hier analysierten Form nur
hochabstrakte Modelle darstellen, zu denen es die verschiedensten
Modifikationen, Zwischenstufen und Ergänzungen gibt, die bei konkreten
Entscheidungen über die Verfassung einer Gesellschaft in die Überlegungen mit
einzubeziehen. {663} wären. [[2] Dies betonen DAHL/LINDBLOM 1963, S.6ff.]
So gibt es nicht nur die Alternative, das private
Eigentum als unbeschränktes Verfügungsrecht beizubehalten oder es ganz
abzuschaffen, sondern es sind verschiedene Zwischenstufen in Form normativer
Beschränkungen des Verfügungsrechts der Eigentümer denkbar, z. B. durch die
Möglichkeiten staatlicher Gesetzgebung in Form von Arbeitsrecht,
Unternehmensrecht, Bodenrecht, Mietrecht oder Kartellrecht.
Weiterhin könnte man
versuchen, die Auswirkungen der systemimmanenten Tendenz zur ungleichen
Verteilung der Einkommen durch gesetzlich geregelte Umverteilungen über
Steuergesetze, Sozialgesetze oder Subventionsgesetze zu mildern.
Ob nun in einer bestimmten Gesellschaft zu einem bestimmten
Zeitpunkt ein derartig "demokratisch gebändigter Kapitalismus" eine bessere
Annäherung an das Gesamtinteresse erzielt als z. B. eine "sozialistische
Marktwirtschaft" mit öffentlichem Eigentum an den sachlichen
Produktionsfaktoren, kann nicht durch eine pauschale Gegenüberstellung von
Tauschprinzip und Mehrheitsprinzip entschieden werden. Dazu müssen die beiden
Alternativen als vollständige Systeme analysiert werden, einschließlich der
Ausgangsbedingungen personeller und technologischer Art. Insbesondere müssen
dazu genauer die Informations- und Motivationsprobleme derartig hochkomplexer
Entscheidungs-Systeme ökonomisch-politischer Art in die Untersuchung mit
einbezogen werden. Für einen solchen Vergleich konkreter Institutionen-Systeme
in normativer Absicht kann die vorliegende Arbeit zumindest die theoretischen
Grundlagen liefern.{664}
LITERATUR - VERZEICHNIS
Zur Erläuterung: Bei Aufsätzen wurde der Titel in Anführungszeichen gesetzt. Ihr erstes Erscheinen wird durch die eingeklammerte Jahreszahl angegeben. Der Ausdruck "Zitiert nach Wiederabdruck" wird abgekürzt mit "Z. n. W.". Bei Büchern wurde zur Information das Jahr des erstmaligen Erscheinens in Klammern hinzugefügt. Die Auflage wird durch die hochgestellte Zahl unmittelbar vor dem Erscheinungsjahr angegeben.
ALBERT, H.: "Modell-Platonismus: Der neoklassische Stil des ökonomischen Denkens in kritischer Beleuchtung" (1963). Z. n. W. in: ALBERT 1967, S.331-367.
ALBERT, H.: Marktsoziologie und Entscheidungslogik. Neuwied u. a. 1967
ALBERT, H.: Traktat über kritische Vernunft. Tübingen 21969 (11968)
ALBIN, P.S.: "Economic Values and the Value of Human Life" in: HOOK 1967, S.94-100
ALCHIAN, A.: "The Meaning of Utility Measurement" (1953). Z. n. W. in: TOWNSEND 1971, S.123-154
ALTVATER, E. u.a.: Materialien zur Kritik der bürgerlichen Ökonomie. Giessen 1971 {665}
APEL, K.O.: "Das Apriori der Kommunikationsgemeinschaft und die Ethik" (1967). Z. n. W. in: APEL 1973, Bd.2, S.358-435
APEL, K.O.: Transformation der Philosophie. 2 Bde. Frankfurt a. M. 1973
ARMSTRONG, W.E.: "Utility and the Theory of Welfare" in: Oxford Economic Papers N.S. 3.(1951) S.259ff.
ARNASZUS, H.: Spieltheorie und Nutzenbegriff aus marxistischer Sicht. Frankfurt a. M. 1974
ARROW, K.J.: "Values and Collective Decision-Making" (1967). Z. n. W. in: PHELPS 1973, S.117-136
ARROW, K.J.: Social Choice and Individual Values. 21963 (11951)
ARROW, K.J. / T. SCITOVSKY (Hg.): Readings in Welfare Economics. London u. a. 1969
AYER, A.J.: Sprache, Wahrheit und Logik. Stuttgart 1970 (11935)
AYER, A.J.: "Die praktische Funktion moralischer Urteile" (1954). Z. n. W. in: BIRNBACHER / HOERSTER 1976, S.55-67
BACHRACH, P. / M.S. BARATZ: "Two Faces of Power" (1962). Z. n. W. in: CASTLES u. a. 1971, S.376-388.
BAIER, K.: "Der moralische Standpunkt" (1954). Z. n. W. in: GREWENDORF / MEGGLE 1974, S.285-316 {666}
BAIER, K.: "Welfare and Preference" in: HOOK 1967, S. 120-135
BANNOCK, G. / R.E. BAXTER / R. REES: The Penguin Dictionary of Economics. Harmondsworth 1972
BARKER, E.: Reflections on Government. London u. a. 1967 (11942)
BARRY, B.: "Justice and the Common Good" (1960/61). Z. n. W. in: QUINTON 1967, 5.189-193
BARRY, B.: "The Public Interest" (1964). Z. n. W. in: QUINTON 1967, S.112-126
BARRY, B.: The Liberal Theory of Justice. A critical examination of the principal doctrines in 'A Theory of Justice' by John RAWLS. Oxford 1973
BATOR, F.M.: "The Simple Analytics of Welfare Maximization" (1957). Z. n. W. in: TOWNSEND 1971, S.372-420
BATOR, F.M.: "The Anatomy of Market Failure" in: Quarterly Journal of Economics 72.(1958) S.351-379
BAUMOL, W.J.: "The Cardinal Utility which is Ordinal" in: Economic Journal 68.(1958) S.665ff.
BAY, Chr.: The Structure of Freedom. Stanford 1970 (11965)
BENN, S.I. / R.S. PETERS: Social Principles and the Democratic State. London 1959 {667}
BENTHAM, J.: Introduction to the Principles of Morals and Legislation (11789). Z. n. W. in: WARNOCK 1962, S.33-77
BERGSON, A.: "A Reformulation of Certain Aspects of Welfare Economics" (1938). Z. n. W. in: ARROW / SCITOVSKY 1969, S.7-25
BERKEMANN, J.: "Zum Prinzip der Widerspruchsfreiheit in der deontischen Logik" in: LENK 1974, S.166-197
BERNHOLZ, P.: Grundlagen der Politischen Ökonomie. Bd.1 . Tübingen 1972
BINDRA, D. / J. STEWART (Hg.) : Motivation. Harmondsworth 1966
BIRNBACHER, D. / N. HOERSTER (Hg.): Texte zur Ethik. München 1976
BLACK, D.: "On the Rationale of Group Decision-Making" in: Journal of Political Economy 56. (1948) S.23-34
BLACK, D.: The Theory of Committees and Elections. London 1971 (11958)
BLACK, D. / R.A. NEWING: Committee Decisions with Complementary Valuation. London 1951
BLAUG, M.: Economic Theory in Retrospect. London 1968
BOSANQUET, B.: The Philosophical Theory of the State. London u. a. 1965 (11899)
BOULDING, K.E.: "Einführung in die Wohlfahrtsökonomik" (1952). Z. n. W. in: GÄFGEN 1966, S.77-109 {668}
BRANDT, R.B.: "The Concept of Welfare" in: KRUPP 1966, S.257-276
BUCHANAN, J. / G. TULLOCK: The Calculus of Consent. Logical Foundations of Constitutional Democracy. Ann Arbor 1969 (11962)
BURSTEIN, M.L.: "The Index Number Problem" (1963). Z. n. W. in: CLOWER 1969, S.61-64
CASTLES, F.G. u. a. (Hg.): Decisions, Organizations, and Society. Harmondsworth 1971
CHASE, S.B. (Hg.): Problems in Public Expenditure Analysis. Washington 1968
CHIPMAN, J.S.: "The Nature and Meaning of Equilibrium in Economic Theory" (1965). Z. n. W. in: TOWNSEND 1971, S.341-371
CLAUSS, G. / H. EBNER: Grundlagen der Statistik. Frankfurt a. M. 1970
CLOWER, R.W. (Hg.): Monetary Theory. Harmondsworth 1969
CODDINGTON, A.: Theories of the Bargaining Process. London 1968
COLLARD, D.: Prices, Markets and Welfare. London 1972
DAHL, R.A.: Modern Political Analysis. Englewood Cliffs N.J. 1963 {669}
DAHL, R.A.: A Preface to Democratic Theory. Chicago u. a. 111970 (11956)
DAHL, R.A. / Ch.E. LINDBLOM: Politics, Economics, and Welfare. Planning and Politico-Economic Systems Resolved into Basic Social Processes. New York u. a. 1963 (11953)
DEBORIN, A. / N. BUCHARIN: Kontroversen über dialektischen und mechanistischen Materialismus. Einleitung von 0. NEGT. Frankfurt a. M. 1969
DENNINGER, E.: Staatsrecht 1. Einführung in die Grundprobleme des Verfassungsrechts der Bundesrepublik Deutschland. Reinbek 1973
DODGSON, C.L.: "A Discussion of the Various Methods of Procedure in Conducting Elections" (1873). Z. n. W. in: BLACK 1971, S.214-222
DODGSON, C.L.: "Suggestions as to the Best Method of Taking Votes, Where More than Two Issues are to be Voted on" (1874). Z. n. W. in: BLACK 1971, S.222-224
DODGSON, C.L.: "A Method of Taking Votes an More than Two Issues" (1876). Z. n. W. in: BLACK 1971, S.224-234
DOLLARD, J. / N.E. MILLER: Personality and Psychotherapy. An Analysis in Terms of Learning, Thinking, and Culture. New York u. a. 1950
DORFMAN, R.: The Price System. Englewood Cliffs N.J. 1964 {670}
DOWNS, A.: Ökonomische Theorie der Demokratie. Tübingen 1968 (11957)
DOWNS, A.: "In Defence of Majority Voting" in: Journal of Political Economy 69.(1961) S.192-199
EICHHORN, W.P.: Stichwort "Norm" in: KLAUS / BUHR 81971, S.793-796
ENGELS, F.: Herrn Eugen Dührings Umwälzung der Wissenschaft (Anti-Dühring) (11878). Z. n. W. in: MARX / ENGELS 1972, S.5-303
EYSENCK, H.-J. / S. RACHMAN: Neurosen - Ursachen und Heilmethoden. Einführung in die moderne Verhaltenstherapie. Berlin (DDR) 1968 (11965)
FACH, W.: Koalition und Opposition in spieltheoretischer Sicht. Ein Beitrag zur Analyse und Kritik der Neuen Politischen Ökonomie. Berlin (West) 1974
FARQUHARSON, R.: Theory of Voting. Oxford 1969 (11961)
FECHNER, G.Th.: Elemente der Psychophysik. Leipzig 1889
FOERDERREUTHER, U. u. a.: "Gesamtwirtschaftliche Grundbegriffe und -beziehungen. I. Teil: Wert- und Preislehre" in: Mehrwert Nr.1, Erlangen 1972
FOOT, Ph. (Hg.): Theories of Ethics. London u. a. 1967
FRAENKEL, E.: "Der Pluralismus als Strukturelement der freiheitlich rechtsstaatlichen Demokratie" (1964) Z. n. W. in: FRAENKEL 1974, S.197-221 {671}
FRAENKEL, E.: Deutschland und die westlichen Demokratien. Stuttgart u. a. 61974 (11964)
FRANKENA, W.K.: "The Naturalistic Fallacy" (1939). Z. n. W. in: FOOT 1967, S.50-63
FRANKENA, W.K.: Analytische Ethik. Eine Einführung. München 1972 (11963)
FREUD, S.: Vorlesungen zur Einführung in die Psychoanalyse und Neue Folge. Frankfurt a. M. 1969 (11916/17 u. 11933)
FREY, B.S.: Umweltökonomie. Göttingen 1972
FRIEDRICH, W. (Hg.): Methoden der marxistisch-leninistischen Sozialforschung. Berlin (DDR) 1970
GÄFGEN, G. (Hg.): Grundlagen der Wirtschaftspolitik. Köln u. a. 1966
GÄFGEN, G.: Theorie der wirtschaftlichen Entscheidung. Untersuchungen zur Logik und ökonomischen Bedeutung des rationalen Handelns. Tübingen 21968 (11963)
GARMAN, M. und M. KAMIEN: "The Paradox of Voting: Probability Calculations" in: Behavioral Science 13.(1968)
GAUTHIER, D.P.: "Morality and Advantage" (1967). Z. n. W. in: GAUTHIER 1970, S.166-180
GAUTHIER, D.P. (Hg.): Morality and Rational Self-Interest. Englewood Cliffs N.J. 1970 {672}
GEIGER, Th.: "Kritische Bemerkungen zum Begriff der Ideologie" (1949). Z. n. W. in LENK 1971, S.228-234
GEISMANN, G.: Ethik und Herrschaftsordnung. Ein Beitrag zum Problem der Legitimation. Tübingen 1974
GELLNER, E.A.: "Ethik und Logik" (1954/55). Z. n. W.; in: GREWENDORF / MEGGLE 1974, S.175-197
GEORGESCU-ROEGEN, N.: "Choice, Expectations, and Measurability" in: Quarterly Journal of Economics 58.(1954) S.503-534
GÖRLITZ, A. (Hg.): Handlexikon zur Rechtswissenschaft. Reinbek 1974 (11972)
GOODMAN, L.A. / H. MARKOWITZ: "Social Welfare Functions Based on Individual Rankings" in: American Journal of Sociology 58.(1952) S.257ff.
GREEN, H.A.J.: Consumer Theory. Harmondsworth 1971
GREWENDORF, G. / G. MEGGLE (Hg.) : Seminar: Sprache und Ethik. Zur Entwicklung der Metaethik. Frankfurt a. M. 1974
HABERMAS, J.: Theorie und Praxis. Sozialphilosophische Studien. Frankfurt a. M. 41971 (11963)
HABERMAS, J.: Legitimationsprobleme im Spätkapitalismus. Frankfurt a. M. 1973
HABERMAS, J. / N. LUHMANN: Theorie der Gesellschaft oder Sozialtechnologie. Frankfurt a. M. 1971 {673}
HARE, R.M.: "Universalisierbarkeit" (1954/55). Z. n. W. in: GREWENDORF / MEGGLE 1974, S.198-216
HARE, R.M.: The Language of Morals. London u. a. 1964 (11952)
HARE, R.M.: Freedom and Reason. London u. a. 1965 (11963)
HARSANYI, J.C.: "Messung der sozialen Macht" (1962). Z. n. W. in: SHUBIK 1965, S.190-215
HARSANYI, J.C.: "Welfare Economics of Variable Tastes" in: Review of Economic Studies 21.(1953/54) S.204-213
HARSANYI, J.C.: "Cardinal Welfare, Individualistic Ethics, and Interpersonal Comparisons of Utility" (1955). Z. n. W. in: PHELPS 1973, S.266-285
HEBB, D.O.: Einführung in die moderne Psychologie. Weinheim u. a. 1967 (11958)
HENDERSON, J.M. / R.E. QUANDT: Microeconomic Theory. A Mathematical Approach. New York u. a. 1958
HENNIG, W.: "Gütekriterien als Präzisionsbedingungen sozialwissenschaftlicher Forschungsmethoden" in: FRIEDRICH 1970, S.243-263
HEUER, U.-J. u. a.: Sozialistisches Wirtschaftsrecht - Instrument der Wirtschaftsführung. Berlin (DDR) 1971
HEUER, U.-J.: Gesellschaftliche Gesetze und politische Organisation. Berlin (DDR) 1974 {674}
HOBBES, Th.: Leviathan. Hg. von C.B. MacPHERSON. Harmondsworth 1968 (11651)
HOFMANN, W.: Wert- und Preislehre. Berlin (West) 21971 (11964 )
HOOK, S. (Hg.): Human Values and Economic Policy. A Symposium. New York 1967
HORN, K.: "Zur politischen Psychologie des Faschismus in Deutschland" (1970). Z. n. W. in: KÜHNL 1974, S.164-175
HUME, D.: A Treatise of Human Nature. Hg. von E.C. MOSSNER. Harmondsworth 1969 (11739 u. 11740)
HUME, D.: Enquiries Concerning the Human Understanding and Concerning the Principles of Morals. Hg. von L.A. SELBY-BIGGE. London u. a. 1970 (11748 u. 11751)
HUNT, E.K. / J.G. SCHWARTZ (Hg.): A Critique of Economic Theory. Harmondsworth 1972
ILTING, K.H.: "Anerkennung" in: Probleme der Ethik, Freiburg 1972
JEVONS, W.S.: "Barter" (1910). Z. n. W. in: CLOWER 1969, S.25-29
JEVONS, W.S.: The Theory of Political Economy. Hg. von R.D.C. BLACK. Harmondsworth 1970 (11871)
KADE, G.: Die Grundannahmen der Preistheorie. Berlin u.a. 1962 {675}
KALDOR, N.: "Welfare Proposititions of Economics and Interpersonal Comparisons of Utility" (1939). Z. n. W. in: ARROW / SCITOVSKY 1969, S.387-389
KAMBARTEL, F.: "Wie ist praktische Philosophie konstruktiv möglich? Über einige Missverständnisse eines methodischen Verständnisses praktischer Diskurse" (1974a) in: KAMBARTEL 1974c, S.9-33
KAMBARTEL, F.: "Moralisches Argumentieren - Methodische Analysen zur Ethik" (1974b). In: KAMBARTEL 1974c, S.54-72
KAMBARTEL, F. (Hg.): Praktische Philosophie und konstruktive Wissenschaftstheorie. Frankfurt a. M. 1974c
KANT, I.: Kritik der praktischen Vernunft. Stuttgart 1966 (11788)
KANT, I.: Grundlegung zur Metaphysik der Sitten. Stuttgart 1967 (11785)
KAPP, K.W.: "Nationalökonomie und rationaler Humanismus" in: KYKLOS 21.(1968) S.1-25
KAPP, W.K.: The Social Costs of Private Enterprise. New York 1971 (11950)
KAUTSKY, K.: "Ethik und materialistische Geschichtsauffassung" (1906). Z. n. W. in: SANDKÜHLER / VEGA 1974, S.193-261
KELSEN, H.: The Pure Theory of Law. Berkeley 1970 (11934) {676}
KINSEY, A.C. u.a.: Das sexuelle Verhalten der Frau. Berlin (West) u. a. 1963 (11953)
KLAUS, G.: Die Macht des Wortes. Ein erkenntnistheoretisch-pragmatisches Traktat. Berlin (DDR) 41968 (11964)
KLAUS, G.: Spieltheorie in philosophischer Sicht. Berlin (DDR) 1968
KLAUS, G. / M. BUHR (Hg.): Philosophisches Wörterbuch. Berlin (West) 81971 (11964)
KÖRNER, S.: Kant. Göttingen 1967 (11955)
KOLAKOWSKI, L.: Die Philosophie des Positivismus. München 1971 (11966)
KRAFT, V.: Die Grundlagen einer wissenschaftlichen Wertlehre. Wien 21951 (11937)
KRASEMANN, I. / G. KOCH u.a.: Politisches Grundwissen. Berlin (DDR) 1970
KRUPP, S.R. (Hg.): The Structure of Economic Science. Essays on Methodology. Englewood Cliffs N.J. 1966
KÜHNL, R. (Hg.): Texte zur Faschismusdiskussion I. Positionen und Kontroversen. Reinbek 1974
KÜLP, B.: Grundfragen der Wirtschaft. Eine Einführung in die Sozialökonomie. Köln 1967
KÜLP, B. u.a.: Wohlfahrtsökonomik I. Die Wohlfahrtskriterien. Tübingen 1975 {677}
KUTSCHERA, F. v.: Einführung in die Logik der Normen, Werte und Entscheidungen. Freiburg u. a. 1973
LANGE, 0.: On the Economic Theory of Socialism. (1938) Z. n. W. in NOVE / NUTI 1972, S.92-110
LANGE, 0.: Einführung in die Ökonometrie. Berlin (DDR) 21968 (11958)
LASLETT, P. / W.G. RUNCIMAN (Hg.): Philosophy, Politics, and Society. 2. Series. Oxford 1962
LAYARD, R. (Hg.): Cost-Benefit Analysis. Harmondsworth 1972
LEIBENSTEIN, H.: "Notes on Welfare Economics and the Theory of Democracy" in: Economic Journal 72.(1962) S.299-319
LENK, H. (Hg.): Normenlogik. München 1974
LENK, K. (Hg.): Ideologie. Ideologiekritik und Wissenssoziologie. Neuwied u. a. 51971 (11961)
LITTLE, I.M.D.: A Critique of Welfare Economics. London u. a. 21970 (11950)
LOCKE, J.: Two Treatises of Government. Hg. von P. LASLETT. New York u. a. 1965 (11689/90)
LORENZEN, P.: "Szientismus versus Dialektik" (1969). Z. n. W. in: KAMBARTEL 1974c, S.34-53
LORENZEN, P.: "Grundlagen der praktischen Philosophie" (1970). Z. n. W. in: LORENZEN 1974, S.22-46 {678}
LORENZEN, P.: Konstruktive Wissenschaftstheorie. Frankfurt a. M. 1974
LUCE, R.D. / H. RAIFFA: Games and Decisions. Introduction and Critical Survey. New York u. a. 1957
LUHMANN, N.: "Normen in soziologischer Perspektive" in: Soziale Welt 20.(1969) S.28-18
MacINTYRE, A.: "What Morality is not" (1957). Z. n. W. in: WALLACE / WALKER 1970, S.26-39
MACKSCHEIDT, K.: Zur Theorie des optimalen Budgets. Tübingen 1973
MacPHERSON, C.B.: Die politische Theorie des Besitzindividualismus. Von HOBBES bis LOCKE. Frankfurt a. M. 1967 (11962)
MacCORQUODALE, K. / P.E. MEEHL: "Hypothetical Constructs and Intervening Variables" in: Psychological Review 55.(1918)
MARSCHAK, J.: "Nutzenmessung und Wahrscheinlichkeit" (1951). Z. n. W. in: SHUBIK 1965, S.103-116
MARSHALL, A.: Principles of Economics. London u. a. 81972 (1189o)
MARX, K.: Das Kapital. Kritik der politischen Ökonomie. Bd.1. (11867). Z. n. W. in: MARX / ENGELS 1968
MARX, K.: "Kritik des Gothaer Programms" (1875). Z. n. W. in MARX / ENGELS 1971, S.333-319{679}
MARX, K. / F. ENGELS: Die deutsche Ideologie (1845/46). Z. n. W. in: MARX / ENGELS 1969, S.9-530
MARX, K. / F. ENGELS: Werke. Hg. vom Institut für Marxismus-Leninismus beim ZK der SED. Berlin (DDR), Bd. 3 1969, Bd. 20 1972, Bd. 23 1968
MARX, K. / F. ENGELS: Ausgewählte Werke. Moskau 1971
MAY, K.O.: "A Set of Independent, Necessary and Sufficient Conditions for Simple Majority Decision" in: Econometrica 20.(1952) S.680-684
MAYNTZ, R. / K. HOLM / P. HÜBNER: Einführung in die Methoden der empirischen Soziologie. Köln u. a. 1969
McCORMICK, B.J.: Wages. Harmondsworth 1969
McKEAN, R.N.: "The Use of Shadow Prices" (1968). Z. n. W. in: LAYARD 1972, S.119-139
MEADE, J.E.: Die stationäre Wirtschaft. Köln 1971 (11965)
MELDEN, A.I. (Hg.): Essays in Moral Philosophy. Seattle u. a. 1958
MILL, J.St.: On Liberty. Representative Government. The Subjection of Women. London 1969 (11859,11861 u. 11869) {680}
MODEL, 0. und C. CREIFELDS: Staatsbürger-Taschenbuch. München 121973
MOORE, G.E.: Principia Ethica. Stuttgart 1970 (11903)
MOORE, G.E.: Ethics. London 1972 (11912)
MÜCKENBERGER, U.: Stichwort "Vertrag" in: GÖRLITZ 1974, S.497-504
MUELLER, D.C.: "Constitutional Democracy and Social Welfare" in: Quarterly Journal of Economics 87.(1973) S.60-80
MURAKAMI, Y: Logic and Social Choice. London u. a. 1968
MUSGRAVE, R.A.: The Theory of Public Finance. A Study in Public Economy. Tokyo u. a. 1959
MYRDAL, G.: Das politische Element in der nationalökonomischen Doktrinbildung. Hannover 1963 (11932)
NEGT, 0.: Soziologie und exemplarisches Lernen. Zur Theorie und Praxis der Arbeiterbildung. Frankfurt a. M. 61971
NEGT, 0.: "Marxismus als Legitimationswissenschaft. Zur Genese der stalinistischen Philosophie". Einleitung zu DEBORIN / BUCHARIN 1969, S.7-50
NELSON, L.: Ausgewählte Schriften. Studienausgabe. Hg. von H.-J. HEYDORN. Frankfurt a. M. 1974
NEUMANN, J.v. / 0. MORGENSTERN: Theory of Games and Economic Behavior. Princeton 21947 {681}
NIEMI, R. / H. WEISBERG: "A Mathematical Solution for the Probability of the Paradox of Voting" in: Behavioral Science 13.(1968)
NOVE, A. / D.M. NUTI (Hg.): Socialist Economics. Harmondsworth 1972
OLSON, M.: Die Logik des kollektiven Handelns. Kollektivgüter und die Theorie der Gruppen. Tübingen 1968 (11965)
OPP, K.-D.: Methodologie der Sozialwissenschaften. Einführung in Probleme ihrer Theoriebildung. Reinbek 1970
PATTANAIK, P.K.: "Risk, Impersonality, and the Social Welfare Function" (1968). Z. n. W. in: PHELPS 1973, S.298-318
PEN, J.: "Bilateral Monopoly, Bargaining and the Concept of Economic Power" (1959). Z. n. W. in: ROTHSCHILD 1971, S.97-115
PHELPS, E.S. (Hg.): Economic Justice. Harmondsworth 1973
PIGOU, A.C.: The Economics of Welfare. London 41948 (11920)
PLAMENATZ, J.P.: Consent, Freedom and Political Obligation. London 21968 (11938)
POPPER, K.R.: The Logic of Scientific Discovery. London 1968 (11934) {682}
POPPER, K.R.: The Open Society and its Enemies. 2 vol. London 51969 (11945)
QUINTON, A. (Hg.): Political Philosophy. London u. a. 1967
RAPOPORT, A.: Strategy and Conscience. New York 1969 (11964)
RAWLS, J.: "Distributive Justice" (1967). Z. n. W. in: PHELPS 1973, S.319-362
RAWLS, J.: A Theory of Justice. London u. a. 1973 (11972)
ROBINSON, J.: Economic Philosophy. Harmondsworth 1966 (11962)
ROTHSCHILD, K.W. (Hg.): Power in Economics. Harmondsworth 1971
ROUSSEAU, J.J.: Der Gesellschaftsvertrag oder die Grundsätze des Staatsrechts. Stuttgart 1968 (11762)
RUSSELL, B.: "Eigeninteresse und allgemeines Wohl" (1910). Z. n. W. in: BIRNBACHER / HOERSTER 1976, S.189-196
RUSSELL, B.: "Ethik" (1927). Z. n. W. in: RUSSELL 1971, S.183-196
RUSSELL, B.: "Über die Verbindlichkeit ethischer Urteile" (1944). Z. n. W. in RUSSELL 1971, S.197-204 {683}
RUSSELL, B.: Dennoch siegt die Vernunft (Human Society in Ethics and Politics). Bonn 1956 (11953)
RUSSELL, B.: Philosophische und politische Aufsätze. Hg. von U. STEINVORTH. Stuttgart 1971
SAMUELSON, P.A.: "Evaluation of Real National Income" (1950). Z. n. W. in: ARROW / SCITOVSKY 1969, S.402-433
SAMUELSON, P.A.: Foundations of Economic Analysis. New York 1965 (11947)
SANDKÜHLER, H.J. / R. de la VEGA (Hg.): Marxismus und Ethik. Frankfurt a. M. 21974 (11970)
SEARLE, J.R.: "How to Derive 'Ought' From 'Is' " (1964). Z. n. W. in: FOOT 1967, S.101-114
SEN, A.K.: Collective Choice and Social Welfare. San Francisco u. a. 1970
SCHLICHT, E.: "Die Theorie der kollektiven Entscheidung und der individualistische Ansatz" in: Leviathan (1974) S.263-279
SCHNEIDER, H.: Mikroökonomie. Eine Einführung in die Preis-, Produktions- und Wohlfahrtstheorie. München 1973
SCHWEMMER, 0.: Philosophie der Praxis. Versuch zur Grundlegung einer Lehre vom moralischen Argumentieren. Frankfurt a. M. 1971
SCHWEMMER, 0.: "Grundlagen einer normativen Ethik" (1973). Z. n. W. in: KAMBARTEL 1974c, S.73-95 {684}
SCHWENGER, H.: Antisexuelle Propaganda. Sexualpolitik in der Kirche. Reinbek 1969
SCITOVSKY, T.: "A Note on Welfare Propositions in Economics" (1941). Z. n. W. in: ARROW / SCITOVSKY 1969, S.390-401
SHUBIK, M. (Hg.) : Spieltheorie und Sozialwissenschaften. Frankfurt a. M. 1965 (11964)
SIMON, H.A.: Administrative Behavior. A Study of Decision-Making Processes in Administrative Organization. New York u. a. 21965 (11945)
SINGER, M.G.: "Moral Rules and Principles" in: MELDEN 1966, S.160-197
SMITH, A.: The Wealth of Nations. Hg. von A. SKINNER. Harmondsworth 1970 (11776)
STEVENSON, Ch.L.: "Faktenkenntnis und moralische Meinungsverschiedenheit" (1963). Z. n. W. in: BIRNBACHER / HOERSTER 1976, S.102-109
STIGLER, G.J.: "The Development of Utility Theory" in: Journal of Political Economy 58.(1950) S.307-327 u. 373-396
TALMON, J.L.: The Origins of Totalitarian Democracy. London 1970 (11952)
TOPITSCH, E.: "Über Leerformeln. Zur Pragmatik des Sprachgebrauchs in Philosophie und politischer Theorie" in: TOPITSCH 1960, S.233ff. {685}
TOPITSCH, E. (Hg.): Probleme der Wissenschaftstheorie. Festschrift für Viktor KRAFT. Wien 1960
TOWNSEND, H. (Hg.): Price Theory. Harmondsworth 1971
TULLOCK, G.: "Problems of Majority Voting" (1959). Z. n. W. in ARROW/SCITOVSKY 1969, S.169-178
VICKREY, W.S.: "Risk, Utility and Social Policy" (1960a). Z. n. W. in: PHELPS 1973, S.286-297
VICKREY, W.S.: "Utility, Strategy, and Social Decision Rules" (1960b). Z. n. W. in: ARROW / SCITOVSKY 1969, S.456-461
WALLACE, G. / A.D.M. WALKER (Hg.): The Definition of Morality. London 1970
WARNOCK, M. (Hg.): Utilitarianism. London 1962
WARNOCK, M.: Ethics Since 1900. London u. a. 21966 (11960)
WEBER, M.: "Die 'Objektivität' sozialwissenschaftlicher und sozialpolitischer Erkenntnis" (1904). Z. n. W. in: WEBER 1968, S.1-64
WEBER, M.: Methodologische Schriften. Studienausgabe. Hg. von J. WINCKELMANN. Frankfurt a. M. 1968.
WEISBROD, B.A.: "Deriving an Implicit Set of Governmental Weights for Income Classes" (1968). Z. n. W. in: LAYARD 1972, S.395-428 {686}
WELLMER, A.: Kritische Gesellschaftstheorie und Positivismus. Frankfurt a. M. 1969
WERNER, R.: Soziale Indikatoren und politische Planung. Reinbek 1975
WOLFELSPERGER, A.: Les Biens Collectifs. Fondement theorique de l'economie publique. Paris 1969
WOLLHEIM, R.: "A Paradox in the Theory of Democracy" in: LASLETT / RUNCIMAN 1962
WINCH, D.M.: Analytical Welfare Economics. Harmondsworth 1971
WRIGHT, G.H.v.: Norm and Action. A Logical Inquiry. London u. a. 1963
ZINN, K.G.: Basistheorie des ökonomischen Wohlstandes in der Demokratie. Die Interdependenz von Gleichheit, Zeit und Nutzen und die verteilungspolitische Konsequenz. Wiesbaden 1970a
ZINN, K.G.: Allgemeine Wirtschaftspolitik als Grundlegung einer kritischen Ökonomie. Stuttgart u. a. 1970b
zurück zu "Tauschprinzip - Mehrheitsprinzip - Gesamtinteresse"
***
zum Anfang
Alphabetische Liste aller Texte
Übersicht
Ethik-Werkstatt: Ende der Seite "Das Mehrheitsprinzip"
Letzte Bearbeitung 14.04.2008 / Eberhard Wesche
Wer diese Website interessant findet, den bitte ich, auch Freunde, Kollegen und Bekannte auf die "Ethik-Werkstatt" hinzuweisen.